
分析 (Ⅰ)根据向量数量积的定义和应用即可求$\overrightarrow a$与$\overrightarrow b$的夹角和|${\overrightarrow a$+$\overrightarrow b}$|的值;
(Ⅱ)根据向量共线的等价条件建立方程关系进行求解即可.
解答 解:(Ⅰ)设$\overrightarrow a$与$\overrightarrow b$的夹角为θ,
∵$(2\overrightarrow a-3\overrightarrow b)•(2\overrightarrow a+\overrightarrow b)=17$∴$4{\overrightarrow a^2}-4\overrightarrow a\overrightarrow{•b}-3{\overrightarrow b^2}=17$,
即4×22-4×2×1×cosθ-3×12=17--------------------------(3分)
∴$cosθ=-\frac{1}{2}$,又∵0≤θ<π,∴$θ=\frac{2π}{3}$.
所以$\overrightarrow a$与$\overrightarrow b$的夹角$\frac{2π}{3}$.--------------------------------------------------(5分)
∵$|\overrightarrow a+\overrightarrow b|=\sqrt{{{(\overrightarrow a+\overrightarrow b)}^2}}=\sqrt{{{\overrightarrow a}^2}+2\overrightarrow a•\overrightarrow b+{{\overrightarrow b}^2}}=\sqrt{{2^2}+2×2×1×cos\frac{2π}{3}+{1^2}}=\sqrt{3}$.
∴$|\overrightarrow a+\overrightarrow b|=\sqrt{3}$.--------------------------------------------------(8分)
(Ⅱ)解:因为$\overrightarrow c$与$\overrightarrow d$共线,所以存在λ,
使$λ\overrightarrow d=\overrightarrow c$$λ(2\overrightarrow a-\overrightarrow b)=m\overrightarrow a+2\overrightarrow b$$(m-2λ)\overrightarrow a+(λ+2)\overrightarrow b=0$
因为$\overrightarrow a$与$\overrightarrow b$不共线,所以 $\left\{\begin{array}{l}m=2λ\\ λ=-2\end{array}\right.$所以,m=-4--------------------------------(12分)
点评 本题主要考查向量数量积的应用以及向量共线的应用,考查学生的运算和转化能力.


科目:高中数学 来源: 题型:解答题
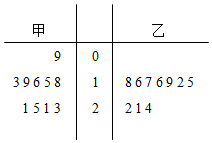 某厂为了解甲、乙两条生产线生产的产品的质量,从两条生产线生产的产品中随机抽取各10件,测量产品中某种元素的含量(单位:毫克).如图是测量数据的茎叶图:
某厂为了解甲、乙两条生产线生产的产品的质量,从两条生产线生产的产品中随机抽取各10件,测量产品中某种元素的含量(单位:毫克).如图是测量数据的茎叶图:查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{5}$ | B. | $\frac{4}{5}$ | C. | ±$\frac{3}{5}$ | D. | -$\frac{4}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | p∨q为假 | B. | p∧q为真 | C. | (¬p)∧q为真 | D. | p∧(¬q)为真 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-3,$\frac{1}{2}$) | B. | (-∞,-3)∪($\frac{1}{2}$,+∞) | C. | (-2,$\frac{1}{3}$) | D. | (-∞,-2)∪($\frac{1}{3}$,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $A_5^5A_5^5$ | B. | $A_4^4A_6^6$ | C. | $A_4^4A_5^5$ | D. | $A_5^5A_6^4$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com