已知函数f(x)=x3+ax2+bx+a2(a,b∈R)
(1)若函数f(x)在x=1处有极值为10,求b的值;
(2)若对任意a∈[-4,+∞),f(x)在x∈[0,2]上单调递增,求b的最小值.
解:(1)f'(x)=3x
2+2ax+bk*s*5*u
则
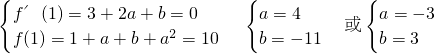
…(5分)
当

时,f'(x)=3x
2+8x-11,△=64+132>0,所以函数有极值点;
当
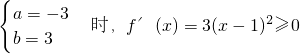
,所以函数无极值点;
则b的值为-11.…(7分)
(2)解法一:f'(x)=3x
2+2ax+b≥0对任意的a∈[-4,+∞),x∈[0,2]都成立
则F(a)=2xa+3x
2+b≥0对任意的a∈[-4,+∞),x∈[0,2]都成立∵x≥0,F(a)在a∈[-4,+∞)单调递增或为常数函数
所以得F(a)
min=F(-4)=-8x+3x
2+b≥0对任意的x∈[0,2]恒成立,
即b≥(-3x
2+8x)
max,又
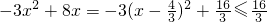
,当
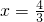
时
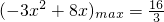
,得
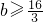
,所以 b的最小值为

. …(15分)
解法二:f'(x)=3x
2+2ax+b≥0对任意的a∈[-4,+∞),x∈[0,2]都成立
即b≥-3x
2-2ax对任意的a∈[-4,+∞),x∈[0,2]都成立,
即b≥(-3x
2-2ax)
max.令
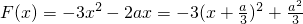
①当a≥0时,F(x)
max=0,∴b≥0;
②当
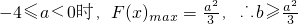
.
又∵
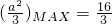
,∴
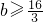
.
综上,b的最小值为

.…(15分)
分析:(1)先对函数求导f'(x)=3x
2+2ax+b,由题意可得f(1)=10,f′(1)=0,结合导数存在的条件可求
(2)解法一:f'(x)=3x
2+2ax+b≥0对任意的a∈[-4,+∞),x∈[0,2]都成立,构造关于a的函数F(a)=2xa+3x
2+b≥0对任意a∈[-4,+∞),x∈[0,2]都成立,结合函数单调性可得F(a)
min=F(-4)从而有b≥(-3x
2+8x)
max,
解法二:f'(x)=3x
2+2ax+b≥0对任意的a∈[-4,+∞),x∈[0,2]都成立,即b≥-3x
2-2ax对任意的a∈[-4,+∞),x∈[0,2]都成立,即b≥(-3x
2-2ax)
max.构造函数
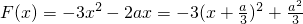
,结合二次函数的性质进行求解函数F(x)的最大值
点评:本题主要考查了利用导数研究函数的极值,利用构造函数的思想把恒成立转化为求解函数的最值问题,要注意构造思想在解题中的应用.

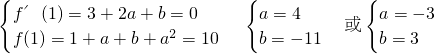 …(5分)
…(5分) 时,f'(x)=3x2+8x-11,△=64+132>0,所以函数有极值点;
时,f'(x)=3x2+8x-11,△=64+132>0,所以函数有极值点;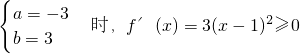 ,所以函数无极值点;
,所以函数无极值点;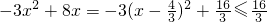 ,当
,当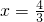 时
时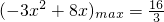 ,得
,得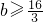 ,所以 b的最小值为
,所以 b的最小值为 . …(15分)
. …(15分)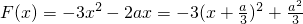
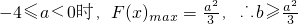 .
.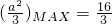 ,∴
,∴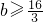 .
. .…(15分)
.…(15分)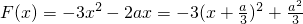 ,结合二次函数的性质进行求解函数F(x)的最大值
,结合二次函数的性质进行求解函数F(x)的最大值

 已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<