
【题目】已知椭圆C: ![]() =1(a>b>0)的离心率为
=1(a>b>0)的离心率为 ![]() ,以原点O为圆心,椭圆C的长半轴为半径的圆与直线2x﹣
,以原点O为圆心,椭圆C的长半轴为半径的圆与直线2x﹣ ![]() y+6=0相切.
y+6=0相切.
(1)求椭圆C的标准方程;
(2)已知点A,B为动直线y=k(x﹣2)(k≠0)与椭圆C的两个交点,问:在x轴上是否存在点E,使 ![]() 2+
2+ ![]()
![]() 为定值?若存在,试求出点E的坐标和定值,若不存在,说明理由.
为定值?若存在,试求出点E的坐标和定值,若不存在,说明理由.
【答案】
(1)解:)由离心率为 ![]() ,得
,得 ![]() =
= ![]() ,
,
即c= ![]() a,①
a,①
又以原点O为圆心,椭圆C的长半轴长为半径的圆为x2+y2=a2,
且与直线 ![]() 相切,
相切,
所以 ![]() ,代入①得c=2,
,代入①得c=2,
所以b2=a2﹣c2=2.
所以椭圆C的标准方程为 ![]() +
+ ![]() =1.
=1.
(2)解:由 ![]() ,可得(1+3k2)x2﹣12k2x+12k2﹣6=0,
,可得(1+3k2)x2﹣12k2x+12k2﹣6=0,
△=144k4﹣4(1+3k2)(12k2﹣6)>0,即为6+6k2>0恒成立.
设A(x1,y1),B(x2,y2),
所以x1+x2= ![]() ,x1x2=
,x1x2= ![]() ,
,
根据题意,假设x轴上存在定点E(m,0),
使得 ![]() 为定值,
为定值,
则有 ![]() =(x1﹣m,y1)(x2﹣m,y2)=(x1﹣m)(x2﹣m)+y1y2
=(x1﹣m,y1)(x2﹣m,y2)=(x1﹣m)(x2﹣m)+y1y2
=(x1﹣m)(x2﹣m)+k2(x1﹣2)(x2﹣2)
=(k2+1)x1x2﹣(2k2+m)(x1+x2)+(4k2+m2)
=(k2+1) ![]() ﹣(2k2+m)
﹣(2k2+m) ![]() +(4k2+m2)
+(4k2+m2)
= ![]() ,
,
要使上式为定值,即与k无关,则应3m2﹣12m+10=3(m2﹣6),
即 ![]() ,此时
,此时 ![]() =
= ![]() 为定值,定点E为
为定值,定点E为 ![]() .
.
【解析】(1)求得圆O的方程,由直线和圆相切的条件:d=r,可得a的值,再由离心率公式,可得c的值,结合a,b,c的关系,可得b,由此能求出椭圆的方程;(2)由直线y=k(x﹣2)和椭圆方程,得(1+3k2)x2﹣12k2x+12k2﹣6=0,由此利用韦达定理、向量的数量积,结合已知条件能求出在x轴上存在点E,使 ![]()
![]() 为定值,定点为(
为定值,定点为( ![]() ,0).
,0).


科目:高中数学 来源: 题型:
【题目】如图所示的茎叶图(图一)为高三某班50名学生的化学考试成绩,图(二)的算法框图中输入的ai为茎叶图中的学生成绩,则输出的m,n分别是( ) 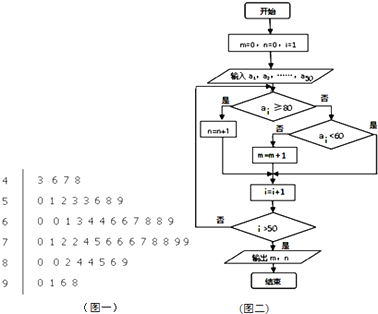
A.m=38,n=12
B.m=26,n=12
C.m=12,n=12
D.m=24,n=10
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个袋中装有大小相同的球10个,其中红球8个,黑球2个,现从袋中有放回地取球,每次随机取1个. 求: (Ⅰ)连续取两次都是红球的概率;
(Ⅱ)如果取出黑球,则取球终止,否则继续取球,直到取出黑球,但取球次数最多不超过4次,求取球次数ξ的概率分布列及期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设抛物线C:y2=3px(p≥0)的焦点为F,点M在C上,|MF|=5,若以MF为直径的圆过点(0,2),则C的方程为( )
A.y2=4x或y2=8x
B.y2=2x或y2=8x
C.y2=4x或y2=16x
D.y2=2x或y2=16x
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知{an}为等差数列,a1+a3+a5=105,a2+a4+a6=99,以Sn表示{an}的前n项和,则使得Sn达到最大值的n是( )
A.21
B.20
C.19
D.18
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知D(x0 , y0)为圆O:x2+y2=12上一点,E(x0 , 0),动点P满足 ![]() =
= ![]() +
+ ![]() ,设动点P的轨迹为曲线C.
,设动点P的轨迹为曲线C.
(1)求曲线C的方程;
(2)若动直线l:y=kx+m与曲线C相切,过点A1(﹣2,0),A2(2,0)分别作A1M⊥l于M,A2N⊥l于N,垂足分别是M,N,问四边形A1MNA2的面积是否存在最值?若存在,请求出最值及此时k的值;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com