
| A. | 若${\overrightarrow a^2}$+${\overrightarrow b^2}$=0,则$\overrightarrow a$=$\overrightarrow b$=$\overrightarrow 0$ | |
| B. | 若k∈R,k$\overrightarrow a$=$\overrightarrow 0$,所以k=0或$\overrightarrow a$=$\overrightarrow 0$ | |
| C. | 若$\overrightarrow a$•$\overrightarrow b$=0,则$\overrightarrow a$=$\overrightarrow 0$或$\overrightarrow b$=$\overrightarrow 0$ | |
| D. | 若$\overrightarrow a$,$\overrightarrow b$都是单位向量,则$\overrightarrow a$•$\overrightarrow b$≤1恒成立 |
分析 根据平面向量的数量积定义及公式进行判断.
解答 解:∵${\overrightarrow{a}}^{2}$+${\overrightarrow{b}}^{2}$=0,${\overrightarrow{a}}^{2}=|\overrightarrow{a}{|}^{2}$≥0,${\overrightarrow{b}}^{2}=|\overrightarrow{b}{|}^{2}$≥0,
∴|$\overrightarrow{a}$|=|$\overrightarrow{b}$|=0,∴$\overrightarrow{a}=\overrightarrow{b}=\overrightarrow{0}$,故A正确;
∵k$\overrightarrow{a}$=$\overrightarrow{0}$,∴k2$|\overrightarrow{a}|$2=0,∴k=0或|$\overrightarrow{a}$|=0,故k=0或$\overrightarrow{a}$=0,
∵$\overrightarrow{a}•\overrightarrow{b}$=|$\overrightarrow{a}$||$\overrightarrow{b}$|cosθ=0,∴|$\overrightarrow{a}$|=0或|$\overrightarrow{b}$|=0或cosθ=0,故$\overrightarrow{a}$=$\overrightarrow{0}$或$\overrightarrow{b}$=$\overrightarrow{0}$或$\overrightarrow{a}⊥\overrightarrow{b}$,故C错误;
∵$\overrightarrow{a},\overrightarrow{b}$是单位向量,∴$\overrightarrow{a}•\overrightarrow{b}$=cosθ≤1,故D错误;
故选:C.
点评 本题考查了平面向量的数量积运算,属于基础题.


 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
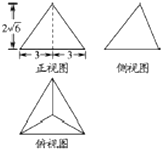
| A. | $9\sqrt{2}$ | B. | 9 | C. | 3$\sqrt{3}$ | D. | 2$\sqrt{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{63}{16}$ | B. | $\frac{63}{16}$ | C. | -$\frac{63}{8}$ | D. | $\frac{63}{8}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | 2-$\frac{\sqrt{2}}{2}$ | D. | 2+$\frac{\sqrt{2}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
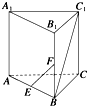 如图所示,在直三棱柱ABC-A1B1C1中,AB=BC=AA1,AB⊥BC,点E、F分别是棱AB、BB1的中点,则直线EF和BC1所成的角是( )
如图所示,在直三棱柱ABC-A1B1C1中,AB=BC=AA1,AB⊥BC,点E、F分别是棱AB、BB1的中点,则直线EF和BC1所成的角是( )| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com