
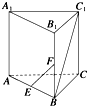
 如图所示,在直三棱柱ABC-A1B1C1中,AB=BC=AA1,AB⊥BC,点E、F分别是棱AB、BB1的中点,则直线EF和BC1所成的角是( )
如图所示,在直三棱柱ABC-A1B1C1中,AB=BC=AA1,AB⊥BC,点E、F分别是棱AB、BB1的中点,则直线EF和BC1所成的角是( )| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
分析 求异面直线所成的角,通过将异面直线的一条平移与另外一条相交,即可求异面直线所成的角.取AC,BC1的中点,M,N,连接EM,MN,FM,证明EF∥MN,那么MN与直线BC1所成的角就是EF和BC1所成的角.
解答 解:取AC,BC1的中点,M,N,连接EM,MN,FN,
∵点E、F分别是棱AB、BB1的中点,
∴EM${\;}_{=}^{∥}\frac{1}{2}$BC,FN${\;}_{=}^{∥}\frac{1}{2}$B1C1,
∵BC=B1C1
∴FN${\;}_{=}^{∥}$EM
所以:四边形EFNM是平行四边形.
则有:EF∥MN.
那么:MN与直线BC1所成的∠BNM就是EF和BC1所成的角.
设:AB=BC=AA1=a,作BC中点G,连接MB,NG,GM.
BN=$\frac{\sqrt{2}}{2}a$,NM=$\frac{\sqrt{2}}{2}a$,BM=$\frac{\sqrt{2}}{2}a$,
△BNM是等边三角形,∠BNM=60°,即EF和BC1所成的角为60°.
故选:C.
点评 本题考查了求异面直线所成的角的证明和计算,属于基础题.


科目:高中数学 来源: 题型:选择题
| A. | 若${\overrightarrow a^2}$+${\overrightarrow b^2}$=0,则$\overrightarrow a$=$\overrightarrow b$=$\overrightarrow 0$ | |
| B. | 若k∈R,k$\overrightarrow a$=$\overrightarrow 0$,所以k=0或$\overrightarrow a$=$\overrightarrow 0$ | |
| C. | 若$\overrightarrow a$•$\overrightarrow b$=0,则$\overrightarrow a$=$\overrightarrow 0$或$\overrightarrow b$=$\overrightarrow 0$ | |
| D. | 若$\overrightarrow a$,$\overrightarrow b$都是单位向量,则$\overrightarrow a$•$\overrightarrow b$≤1恒成立 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①、② | B. | ①③ | C. | ②、③ | D. | ② |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | e1•e2>1 | B. | e1•e2<1 | ||
| C. | e1•e2=1 | D. | e1•e2与1大小不确定 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com