
分析 (1)求导,由抛物线在点A(1,1)处的切线为l的斜率k=k切=y'|x=1=2,由点斜式方程即可求得切线l的方程;
(2)由题意可知求得切线与x和y的轴的焦点,求得c和b的值,由椭圆的性质可知a2=b2+c2,即可求得该椭圆的方程.
解答 解:(1)k切=y'|x=1=2x|x=1=2,…(2分)
切点A(1,1),所以切线l的方程为y-1=2(x-1)
即y=2x-1…(4分)
(2)令y=0,则x=$\frac{1}{2}$,所以切线与x轴的交点为$B(\frac{1}{2},0)$…(5分)
令x=0,则y=-1,所以切线与y轴的交点为C(0,-1)
所以$c=\frac{1}{2},b=1$,
$a=\sqrt{{b^2}+{c^2}}=\frac{{\sqrt{5}}}{2}$
所求椭圆方程为$\frac{{4{x^2}}}{5}+{y^2}=1$.
点评 本题考查利用导数求曲线的切线方程及椭圆的简单性质,考查导数的运算,考查计算能力,属于中档题.


 全能测控期末小状元系列答案
全能测控期末小状元系列答案科目:高中数学 来源: 题型:选择题
| A. | -$\frac{63}{16}$ | B. | $\frac{63}{16}$ | C. | -$\frac{63}{8}$ | D. | $\frac{63}{8}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
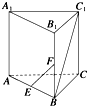 如图所示,在直三棱柱ABC-A1B1C1中,AB=BC=AA1,AB⊥BC,点E、F分别是棱AB、BB1的中点,则直线EF和BC1所成的角是( )
如图所示,在直三棱柱ABC-A1B1C1中,AB=BC=AA1,AB⊥BC,点E、F分别是棱AB、BB1的中点,则直线EF和BC1所成的角是( )| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| x | $\frac{π}{6}$ | $\frac{7π}{6}$ | |||
| ωx+φ | 0 | $\frac{π}{2}$ | π | $\frac{3π}{2}$ | 2π |
| Asin(ωx+φ) | 0 | 2 | 0 | -2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
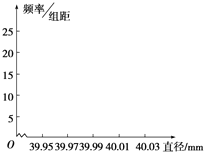 某制造商为运动会生产一批直径为40mm的乒乓球,现随机抽样检查20只,测得每只球的直径(单位:mm,保留两位小数)如下:
某制造商为运动会生产一批直径为40mm的乒乓球,现随机抽样检查20只,测得每只球的直径(单位:mm,保留两位小数)如下:| 分组 | 频数 | 频率 | $\frac{频率}{组距}$ |
| [39.95,39.97) | 2 | 0.10 | 5 |
| [39.97,39.99) | 4 | 0.20 | 10 |
| [39.99,40.01) | 10 | 0.50 | 25 |
| [40.01,40.03] | 4 | 0.20 | 10 |
| 合计 | 20 | 1 | 50 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
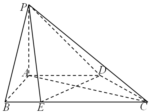 如图,在四棱锥P-ABCD中,直线PA⊥平面ABCD,AD∥BC,AB⊥AD,BC=2AB=2AD=4BE=4.
如图,在四棱锥P-ABCD中,直线PA⊥平面ABCD,AD∥BC,AB⊥AD,BC=2AB=2AD=4BE=4.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com