练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    3．化简$\frac{cos40°}{cos25°\sqrt{1-sin40°}}$=$\sqrt{2}$．

    分析 利用二倍角的余弦函数公式化简，分母中被开方数利用同角三角函数间基本关系，完全平方公式以及二次根式的性质化简，约分后再利用两角和与差的正弦函数公式变形，约分即可得到结果．

    解答 解：原式=$\frac{co{s}^{2}20°-si{n}^{2}20°}{cos25°\sqrt{（cos20°-sin20°）^{2}}}$=$\frac{cos20°+sin20°}{cos25°}$=$\frac{\sqrt{2}cos（45°-20°）}{cos25°}$=$\sqrt{2}$，
    故答案为：$\sqrt{2}$．

    点评 本题考查了同角三角函数间基本关系的运用，熟练掌握基本关系是解本题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

    13．△ABC中，A=$\frac{π}{6}$，b=2，以下命题中正确的序号是①②③．
    ①若a=1，则c有一解；                  
    ②若a=$\sqrt{3}$，则c有两解；
    ③若a=$\frac{11}{6}$，则c有两解；                
    ④若a=3，则c有两解．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    14．已知函数f（x）=25x3+13x2+2016x-5，则f'（0）=2016．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    11．已知a=$\int_0^{\sqrt{6}}$2xdx，则（x-$\frac{1}{x}$）a的二项展开式中常数项为-20．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    18．光线从点A（-2，1）射到x轴后反射到B（4，3）则光线从A到B经过的总路线为（　　）
    A．2$\sqrt{10}$B．2$\sqrt{13}$C．2$\sqrt{11}$D．4$\sqrt{3}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    8．已知集合A={x|x2-4x+3＜0}，B={y|y=x2，x∈R}，则A∩B=（　　）
    A．∅B．[0，1）∪（3，+∞）C．AD．B

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

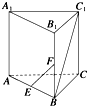    15．如图所示，在直三棱柱ABC-A1B1C1中，AB=BC=AA1，AB⊥BC，点E、F分别是棱AB、BB1的中点，则直线EF和BC1所成的角是（　　）
    A．30°B．45°C．60°D．90°

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    12．某同学用“五点法”画函数f（x）=Asin（ωx+φ）（ω＞0，|φ|＜$\frac{π}{2}$）在某一个周期内的图象时，列表并填入的部分数据如表：
    x$\frac{π}{6}$$\frac{7π}{6}$
    ωx+φ0$\frac{π}{2}$π$\frac{3π}{2}$2π
    Asin（ωx+φ）020-2
    （Ⅰ）请将上表数据补全，并直接写出函数f（x）的解析式；
    （Ⅱ）当x∈[0，$\frac{π}{2}$]时，求函数f（x）的值域．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    13．已知椭圆C1：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的离心率为$\frac{\sqrt{2}}{2}$，且过点（1，$\frac{{\sqrt{2}}}{2}$）．
    （Ⅰ）求C1的方程；
    （Ⅱ）设直线l同时与椭圆C1和抛物线C2：y2=4x相切，求直线l的方程．

    查看答案和解析>>

    同步练习册答案