
【题目】某电脑公司有6名产品推销员,其中工作年限与年推销金额数据如下表:
推销员编号 | 1 | 2 | 3 | 4 | 5 |
工作年限 | 3 | 5 | 6 | 7 | 9 |
推销金额 | 2 | 3 | 4 | 5 | 6 |
(1)请画出上表数据的散点图;

(2)求年推销金额![]() 关于工作年限
关于工作年限![]() 的线性回归方程;
的线性回归方程;
(3)若第6名推销员的工作年限为11年,试估计他的年推销金额.
 ,
,![]() .
.
【答案】(1)散点图见解析;(2)![]() ;(3)5.9万元.
;(3)5.9万元.
【解析】试题分析:(1)根据表格中数据,直接描点即可得到散点图;(2)首先求出![]() 的平均数,利用最小二乘法求出
的平均数,利用最小二乘法求出![]() 的值,再利用样本中心点满足线性回程和前面做出的横标和纵标的平均值,求出
的值,再利用样本中心点满足线性回程和前面做出的横标和纵标的平均值,求出![]() 值,写出线性回归方程;(3)第
值,写出线性回归方程;(3)第![]() 名推销员的工作年限为
名推销员的工作年限为![]() 年,即
年,即![]() 时,把自变量的值代入线性回归方程,得到
时,把自变量的值代入线性回归方程,得到![]() 的预报值,即估计出第
的预报值,即估计出第![]() 名推销员的年推销金
名推销员的年推销金![]() 万元.
万元.
试题解析:(1)散点图如图所示:
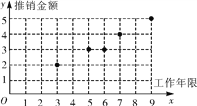
(2)由(1)知y与x具有线性相关关系.![]() =6,
=6,![]() =3.4
=3.4
![]() =200,
=200, ![]() =112, ∴
=112, ∴![]() .
.
∴年推销金额y关于工作年限x的线性回归方程为![]() .
.
(3)由(2)知,当x=11时,![]() =0.4+0.5×11=5.9.可以估计第6名推销员的年推销金额为5.9万元.
=0.4+0.5×11=5.9.可以估计第6名推销员的年推销金额为5.9万元.


科目:高中数学 来源: 题型:
【题目】已知函数![]() ,若
,若![]()
(1)求![]() 的值,并写出函数
的值,并写出函数![]() 的最小正周期(不需证明);
的最小正周期(不需证明);
(2)是否存在正整数![]() ,使得函数
,使得函数![]() 在区间
在区间![]() 内恰有
内恰有![]() 个零点?若存在,求出
个零点?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=(x﹣2)ex+a(x+2)2(x>0).
(1)若f(x)是(0,+∞)的单调递增函数,求实数a的取值范围;
(2)当 ![]() 时,求证:函数f(x)有最小值,并求函数f(x)最小值的取值范围.
时,求证:函数f(x)有最小值,并求函数f(x)最小值的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数 ![]() (
( ![]() 为常数,e=2.71828……是自然对数的底数).
为常数,e=2.71828……是自然对数的底数).
(1)当 ![]() 时,求函数
时,求函数 ![]() 的单调区间;
的单调区间;
(2)若函数 ![]() 在
在 ![]() 内存在两个极值点,求
内存在两个极值点,求 ![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 的一系列对应值如下表:
的一系列对应值如下表:
|
|
|
|
|
|
|
|
| -1 | 1 | 3 | 1 | -1 | 1 | 3 |
(1)根据表格提供的数据画出函数![]() 的图像并求出函数解析式;
的图像并求出函数解析式;
(2)根据(1)的结果,若函数![]() 的周期为
的周期为![]() ,当
,当![]() 时,方程
时,方程![]() 恰有两个不同的解,求实数
恰有两个不同的解,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,其中
,其中![]() ,记函数
,记函数![]() 的定义域为
的定义域为![]() .
.
(1)求函数![]() 的定义域
的定义域![]() ;
;
(2)若函数![]() 的最大值为2,求
的最大值为2,求![]() 的值;
的值;
(3)若对于![]() 内的任意实数
内的任意实数![]() ,不等式
,不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校有教师400人,对他们进行年龄状况和学历的调查,其结果如下:
学历 | 35岁以下 | 35-55岁 | 55岁及以上 |
本科 |
| 60 | 40 |
硕士 | 80 | 40 |
|
(1)若随机抽取一人,年龄是35岁以下的概率为![]() ,求
,求![]() ;
;
(2)在35-55岁年龄段的教师中,按学历状况用分层抽样的方法,抽取一个样本容量为5的样本,然后在这5名教师中任选2人,求两人中至多有1人的学历为本科的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com