
【题目】在一次购物抽奖活动中,假设某10张券中有一等奖券1张,可获价值50元的奖品;有二等奖券3张,每张可获价值10元的奖品;其余6张没有奖,某顾客从此10张券中任抽2张,求:
(1)该顾客中奖的概率;
(2)该顾客获得的奖品总价值X(元)的概率分布列和期望E(X).
【答案】(1)![]() ;(2)分布列见解析,期望为16.
;(2)分布列见解析,期望为16.
【解析】试题分析:
(1)利用对立事件公式可得该顾客中奖的概率为![]() ;
;
(2)由超几何分布求得分布列,然后求解数学期望可得期望值为16.
试题解析:
解法一:(1)P=I-![]() =1-
=1-![]() =
=![]() ,即该顾客中奖的概率为
,即该顾客中奖的概率为![]() .
.
(2)ξ的所有可能值为:0,10,20,50,60(元).P(ξ=0)=![]() =
=![]() ,P(ξ=10)=
,P(ξ=10)=![]() =
=![]() ,
,
P(ξ=20)=![]() =
=![]() ,P(ξ=50)=
,P(ξ=50)=![]() =
=![]() ,P(ξ=60)=
,P(ξ=60)=![]() =
=![]() .
.
ξ | 0 | 10 | 20 | 50 | 60 |
P |
|
|
|
| bn= 8an+1an-16an+1+2an+5=0, |
故ξ有分布列:
从而期望Eξ=0×![]() +10×
+10×![]() +20×
+20×![]() +50×
+50×![]() +60×
+60×![]() =16.
=16.
解法二:(1)P=![]() =
=![]() =
=![]() ,
,
(2)ξ的分布列求法同解法一
由于10张券总价值为80元,即每张的平均奖品价值为8元,从而抽2张的平均奖品价值Eξ=2×8=16(元).


 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案科目:高中数学 来源: 题型:
【题目】给定一个数列{an},在这个数列里,任取m(m≥3,m∈N*)项,并且不改变它们在数列{an}中的先后次序,得到的数列{an}的一个m阶子数列.
已知数列{an}的通项公式为an= ![]() (n∈N* , a为常数),等差数列a2 , a3 , a6是数列{an}的一个3子阶数列.
(n∈N* , a为常数),等差数列a2 , a3 , a6是数列{an}的一个3子阶数列.
(1)求a的值;
(2)等差数列b1 , b2 , …,bm是{an}的一个m(m≥3,m∈N*)阶子数列,且b1= ![]() (k为常数,k∈N* , k≥2),求证:m≤k+1
(k为常数,k∈N* , k≥2),求证:m≤k+1
(3)等比数列c1 , c2 , …,cm是{an}的一个m(m≥3,m∈N*)阶子数列,求证:c1+c1+…+cm≤2﹣ ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线![]() 为参数),
为参数),![]() 为参数).
为参数).
(1)化![]() 的参数方程为普通方程,并说明它们分别表示什么曲线;
的参数方程为普通方程,并说明它们分别表示什么曲线;
(2)若![]() 上的点
上的点![]() 对应的参数为
对应的参数为![]() 为
为![]() 上的动点,求
上的动点,求![]() 的中点
的中点![]() 到直线
到直线![]() 为参数)距离的最小值.
为参数)距离的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某电脑公司有6名产品推销员,其工作年限与推销金额数据如下表:
推销员编号 | 1 | 2 | 3 | 4 | 5 |
工作年限 | 3 | 5 | 6 | 7 | 9 |
推销金额 | 2 | 3 | 3 | 4 | 5 |
(1)求年推销金额![]() 关于工作年限
关于工作年限![]() 的线性回归方程;
的线性回归方程;
(2)若第6名推销员的工作年限为11年,试估计他的年推销金额.
附:线性回归方程![]() 中,
中,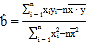 ,
,![]() ,其中
,其中![]() 为样本平均值.
为样本平均值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知 ![]() =(cosα,sinα),
=(cosα,sinα), ![]() =(cosβ,sinβ),0<β<α<π.
=(cosβ,sinβ),0<β<α<π.
(1)若| ![]() ﹣
﹣ ![]() |=
|= ![]() ,求证:
,求证: ![]() ⊥
⊥ ![]() ;
;
(2)设 ![]() =(0,1),若
=(0,1),若 ![]() +
+ ![]() =
= ![]() ,求α,β的值.
,求α,β的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=lnx﹣ax,g(x)=ex﹣ax,其中a为实数.
(1)若f(x)在(1,+∞)上是单调减函数,且g(x)在(1,+∞)上有最小值,求a的取值范围;
(2)若g(x)在(﹣1,+∞)上是单调增函数,试求f(x)的零点个数,并证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】求经过直线L1:3x + 4y – 5 = 0与直线L2:2x – 3y + 8 = 0的交点M,且满足下列条件的直线方程
(1)与直线2x + y + 5 = 0平行 ;
(2)与直线2x + y + 5 = 0垂直;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知向量 ![]() ,其中
,其中![]() .函数
.函数![]() 的图象过点
的图象过点![]() ,点
,点![]() 与其相邻的最高点的距离为4.
与其相邻的最高点的距离为4.
(Ⅰ)求函数![]() 的单调递减区间;
的单调递减区间;
(Ⅱ)计算![]() 的值;
的值;
(Ⅲ)设函数![]() ,试讨论函数
,试讨论函数![]() 在区间 [0,3] 上的零点个数.
在区间 [0,3] 上的零点个数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,将一个各面都涂了油漆的正方体,切割为125个同样大小的小正方体,经过搅拌后,从中随机取一个小正方体,记它的涂漆面数为X,则X的均值E(X)=( )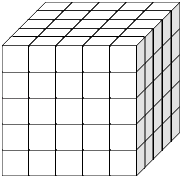
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com