
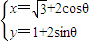 (θ为参数,0≤θ<2π),
(θ为参数,0≤θ<2π),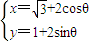 (θ为参数,0≤θ<2π),
(θ为参数,0≤θ<2π),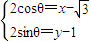 ,两式平方相加得:
,两式平方相加得: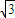 x-2y=0.即为曲线C化为普通方程.
x-2y=0.即为曲线C化为普通方程.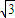 ρcosθ-2ρsinθ=0,
ρcosθ-2ρsinθ=0,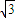 cosθ+2sinθ,即为极坐标系下的极坐标方程.
cosθ+2sinθ,即为极坐标系下的极坐标方程.

科目:高中数学 来源:2014届海南省高二上期末考试文科数学试卷(解析版) 题型:解答题
已知曲线C: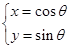 (
(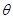 为参数).
为参数).
(1)将C的参数方程化为普通方程;
(2)若把C上各点的坐标经过伸缩变换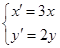 后得到曲线
后得到曲线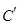 ,求曲线
,求曲线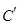 上任意一点到两坐标轴距离之积的最大值.
上任意一点到两坐标轴距离之积的最大值.
查看答案和解析>>
科目:高中数学 来源:2011-2012学年海南省高三上学期教学质量监测考试文科数学 题型:解答题
本小题满分10分)选修4—4:坐标系与参数方程.
已知曲线C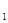 :
: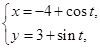 (
(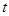 为参数), C
为参数), C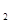 :
: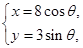 (
(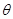 为参数)。
为参数)。
(1)化C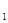 ,C
,C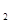 的方程为普通方程,并说明它们分别表示什么曲线;
的方程为普通方程,并说明它们分别表示什么曲线;
(2)若C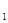 上的点P对应的参数为
上的点P对应的参数为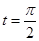 ,Q为C
,Q为C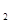 上的动点,求
上的动点,求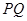 中点
中点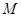 到直线
到直线
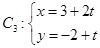 ,(
,(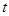 为参数)距离的最小值.
为参数)距离的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
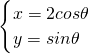 (θ为参数),若A、B是曲线C上关于坐标轴不对称的任意两点.
(θ为参数),若A、B是曲线C上关于坐标轴不对称的任意两点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com