
【题目】已知数列![]() 满足:
满足:![]() (m为正整数),
(m为正整数),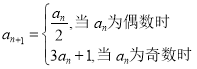 ,若
,若![]() ,则m所有可能的取值为________.
,则m所有可能的取值为________.
【答案】2,3,16,20,21,128
【解析】
采用“倒推”的方式,推导过程中注意分类.
因为![]() ,若
,若![]() 为奇数,则有
为奇数,则有![]() ,无解,若
,无解,若![]() 为偶数,则有
为偶数,则有![]() ,即
,即![]() ;
;
![]() 时,若
时,若![]() 为奇数,则有
为奇数,则有![]() ,无解,若
,无解,若![]() 为偶数,则有
为偶数,则有![]() ,即
,即![]() ;
;
当![]() ;时,若
;时,若![]() 为奇数,则有
为奇数,则有![]() ,
,![]() ,若
,若![]() 为偶数,则有
为偶数,则有![]() ,即
,即![]() ;
;
当![]() 时,若
时,若![]() 为奇数,则有
为奇数,则有![]() ,无解,若
,无解,若![]() 为偶数,则有
为偶数,则有![]() ,即
,即![]() ;
;
当![]() 时,若
时,若![]() 为奇数,则有
为奇数,则有![]() ,无解,若
,无解,若![]() 为偶数,则有
为偶数,则有![]() ,即
,即![]() ;
;
当![]() 时,若
时,若![]() 为奇数,则有
为奇数,则有![]() ,无解,若
,无解,若![]() 为偶数,则有
为偶数,则有![]() ,即
,即![]() ;
;
当![]() 时,若
时,若![]() 为奇数,则有
为奇数,则有![]() ,
,![]() ,若
,若![]() 为偶数,则有
为偶数,则有![]() ,即
,即![]() ;
;
当![]() 时,若
时,若![]() 为奇数,则有
为奇数,则有![]() ,
,![]() ,若
,若![]() 为偶数,则有
为偶数,则有![]() ,即
,即![]() ;
;
当![]() 时,若
时,若![]() 为奇数,则有
为奇数,则有![]() ,无解,若
,无解,若![]() 为偶数,则有
为偶数,则有![]() ,即
,即![]() ;
;
当![]() 时,若
时,若![]() 为奇数,则有
为奇数,则有![]() ,无解,若
,无解,若![]() 为偶数,则有
为偶数,则有![]() ,即
,即![]() ;
;
当![]() 时,若
时,若![]() 为奇数,则有
为奇数,则有![]() ,无解,若
,无解,若![]() 为偶数,则有
为偶数,则有![]() ,即
,即![]() ;
;
当![]() 时,若
时,若![]() 为奇数,则有
为奇数,则有![]() ,无解,若
,无解,若![]() 为偶数,则有
为偶数,则有![]() ,即
,即![]() ;
;
当![]() 时,若
时,若![]() 为奇数,则有
为奇数,则有![]() ,
,![]() ,若
,若![]() 为偶数,则有
为偶数,则有![]() ,即
,即![]() ;
;
当![]() 时,若
时,若![]() 为奇数,则有
为奇数,则有![]() ,
,![]() ,若
,若![]() 为偶数,则有
为偶数,则有![]() ,即
,即![]() ;
;
综上:![]() 可取的值有:2,3,16,20,21,128.
可取的值有:2,3,16,20,21,128.
故答案为:2,3,16,20,21,128


科目:高中数学 来源: 题型:
【题目】已知双曲线C1:![]() -
-![]() =1.
=1.
(1)若点M(3,t)在双曲线C1上,求M点到双曲线C1右焦点的距离;
(2)求与双曲线C1有共同渐近线,且过点(-3,2![]() )的双曲线C2的标准方程.
)的双曲线C2的标准方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知离心率为![]() 的椭圆
的椭圆![]() 焦点在
焦点在![]() 轴上,且椭圆
轴上,且椭圆![]() 个顶点构成的四边形面积为
个顶点构成的四边形面积为![]() ,过点
,过点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 相交于不同的两点
相交于不同的两点![]() 、
、![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)设![]() 为椭圆上一点,且
为椭圆上一点,且![]() (
(![]() 为坐标原点).求当
为坐标原点).求当![]() 时,实数
时,实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某城镇社区为了丰富辖区内广大居民的业余文化生活,创建了社区“文化丹青”大型活动场所,配备了各种文化娱乐活动所需要的设施,让广大居民健康生活、积极向上.社区最近四年内在“文化丹青”上的投资金额统计数据如表:(为了便于计算,把2015年简记为5,其余以此类推)
年份 | 5 | 6 | 7 | 8 |
投资金额 | 15 | 17 | 21 | 27 |
(1)利用所给数据,求出投资金额![]() 与年份
与年份![]() 之间的回归直线方程
之间的回归直线方程![]() ;
;
(2)预测该社区在2019年在“文化丹青”上的投资金额.
(附:对于一组数据![]() ,
, ![]() ,…,
,…, ![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为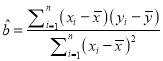 ,
, ![]() .)
.)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国古代数学名著《算法统宗》中有如下问题:“远望巍巍塔七层,红光点点倍加增,共灯三百八十一,请问尖头几盏灯?”意思是:一座7层塔共挂了381盏灯,且相邻两层中的下一层灯数是上一层灯数的2倍,则塔的顶层共有灯( )
A. 1盏 B. 3盏 C. 5盏 D. 9盏
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,岛![]() 、
、![]() 相距
相距![]() 海里.上午9点整有一客轮在岛
海里.上午9点整有一客轮在岛![]() 的北偏西
的北偏西![]() 且距岛
且距岛![]()
![]() 海里的
海里的![]() 处,沿直线方向匀速开往岛
处,沿直线方向匀速开往岛![]() ,在岛
,在岛![]() 停留
停留![]() 分钟后前往
分钟后前往![]() 市.上午
市.上午![]() 测得客轮位于岛
测得客轮位于岛![]() 的北偏西
的北偏西![]() 且距岛
且距岛![]()
![]() 海里的
海里的![]() 处,此时小张从岛
处,此时小张从岛![]() 乘坐速度为
乘坐速度为![]() 海里/小时的小艇沿直线方向前往
海里/小时的小艇沿直线方向前往![]() 岛换乘客轮去
岛换乘客轮去![]() 市.
市.

(Ⅰ)若![]() ,问小张能否乘上这班客轮?
,问小张能否乘上这班客轮?
(Ⅱ)现测得![]() ,
, ![]() .已知速度为
.已知速度为![]() 海里/小时(
海里/小时(![]() )的小艇每小时的总费用为(
)的小艇每小时的总费用为(![]() )元,若小张由岛
)元,若小张由岛![]() 直接乘小艇去
直接乘小艇去![]() 市,则至少需要多少费用?
市,则至少需要多少费用?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com