
| A. | x1>x2 | B. | x1<x2 | C. | x12<x22 | D. | |x1|>|x2| |
分析 先研究函数的性质,观察知函数是个偶函数,由于f′(x)=2x+sinx,在[0,π]上f′(x)>0,当-π<x<0时,f'(x)<0,可推断出当f(x1)<f(x2)时,得f(|x1|)<f(|x2|),从而得解.
解答 解:∵f(x)是偶函数,
又∵f'(x)=2x+sinx,
∴当0<x<π时,f'(x)>0,f(x)单调增;
∴当-π<x<0时,f'(x)<0,f(x)单调减;
所以当f(x1)<f(x2)时,得f(|x1|)<f(|x2|)
所以x12<x22.
故选:C.
点评 本题考查函数的性质奇偶性与单调性,属于利用性质推导出自变量的大小的问题,主要考查函数与导数等基础知识,考查运算求解能力、推理论证能力,考查分类与整合思想、化归与转化思想,属于中档题.


科目:高中数学 来源: 题型:解答题
 如图,在四棱锥P-ABCD中,侧面PAD是正三角形,底面ABCD直角梯形,AD∥BC,∠ADC=90°,AD=2BC=2,$CD=\sqrt{3}$,平面PAD⊥底面ABCD,若M为AD的中点.
如图,在四棱锥P-ABCD中,侧面PAD是正三角形,底面ABCD直角梯形,AD∥BC,∠ADC=90°,AD=2BC=2,$CD=\sqrt{3}$,平面PAD⊥底面ABCD,若M为AD的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在五面体ABCDEF中,四边形ABCD为正方形,EF∥AD,平面ADEF⊥平面ABCD,且BC=2EF,AE=AF,点G是EF的中点.
如图,在五面体ABCDEF中,四边形ABCD为正方形,EF∥AD,平面ADEF⊥平面ABCD,且BC=2EF,AE=AF,点G是EF的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源:2017届四川成都七中高三10月段测数学(理)试卷(解析版) 题型:选择题
已知在 中,
中, ,
, ,
,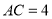 ,
, 是
是 上的点,则
上的点,则 到
到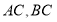 的距离的乘积的最大值为( )
的距离的乘积的最大值为( )
A.3 B.2 C. D.9
D.9
查看答案和解析>>
科目:高中数学 来源:2017届江西省红色七校高三上学期联考一数学(文)试卷(解析版) 题型:选择题
已知函数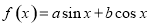 (
( 为常数,
为常数, ,
, )在
)在 处取得最大值,则函数
处取得最大值,则函数 是( )
是( )
A.奇函数且它的图象关于点 对称
对称
B.奇函数且它的图象关于点 对称
对称
C.偶函数且它的图象关于点 对称
对称
D.偶函数且它的图象关于点 对称
对称
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com