
 如图,在五面体ABCDEF中,四边形ABCD为正方形,EF∥AD,平面ADEF⊥平面ABCD,且BC=2EF,AE=AF,点G是EF的中点.
如图,在五面体ABCDEF中,四边形ABCD为正方形,EF∥AD,平面ADEF⊥平面ABCD,且BC=2EF,AE=AF,点G是EF的中点.分析 (Ⅰ)根据等腰三角形AG⊥EF.推证 AG⊥AD,AG⊥平面ABCD,线面的转化 AG⊥CD.
(Ⅱ)根据中点推证GF∥MN,GF=MN.四边形GFNM是平行四边形. 由直线平面平行的判定定理推证GM∥平面ABF;
(Ⅲ)根据中点与平行的关系得出点O为线段GC的中点.
解答  (Ⅰ)证明:因为AE=AF,点G是EF的中点,
(Ⅰ)证明:因为AE=AF,点G是EF的中点,
所以 AG⊥EF.
又因为 EF∥AD,
所以 AG⊥AD.
因为平面ADEF⊥平面ABCD,且平面ADEF∩平面ABCD=AD,AG?平面ADEF,
所以 AG⊥平面ABCD.
因为 CD?平面ABCD,
所以 AG⊥CD.
(Ⅱ)证明:如图,过点M作MN∥BC,且交AB于点N,连结NF,
因为 $\frac{AM}{MC}=\frac{1}{3}$,所以$\frac{MN}{BC}=\frac{AM}{AC}=\frac{1}{4}$,
因为 BC=2EF,点G是EF的中点,
所以 BC=4GF,
又因为 EF∥AD,四边形ABCD为正方形,
所以 GF∥MN,GF=MN.
所以四边形GFNM是平行四边形.
所以 GM∥FN.
又因为GM?平面ABF,FN?平面ABF,
所以 GM∥平面ABF.
(Ⅲ)解:点O为线段GC的中点.
点评 本题考查了空间几何体的性质,空间直线的位置关系,直线平面的平行关系,掌握好定理,转化直线的为关系判断即可.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 奇函数,且在(0,1)上是增函数,在(1,+∞)上是减函数 | |
| B. | 奇函数,且在(0,1)上是减函数,在(1,+∞)上是增函数 | |
| C. | 偶函数,且在(0,1)上是增函数,在(1,+∞)上是减函数 | |
| D. | 偶函数,且在(0,1)上是减函数,在(1,+∞)上是增函数 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x1>x2 | B. | x1<x2 | C. | x12<x22 | D. | |x1|>|x2| |
查看答案和解析>>
科目:高中数学 来源:2017届四川成都七中高三10月段测数学(理)试卷(解析版) 题型:解答题
已知椭圆 的离心率为
的离心率为 ,以
,以 为圆心,椭圆的短半轴长为半径的圆与直线
为圆心,椭圆的短半轴长为半径的圆与直线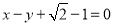 相切.
相切.
(1)求椭圆 的标准方程;
的标准方程;
(2)已知点 ,和面内一点
,和面内一点 ,过点
,过点 任作直线
任作直线 与椭圆
与椭圆 相交于
相交于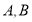 两点,设直线
两点,设直线 的斜率分别为
的斜率分别为 ,若
,若 ,试求
,试求 满足的关系式.
满足的关系式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com