
分析 (1)通过两角和与差的三角函数化简已知条件,然后求解直线l的直角坐标方程.
(2)设点P的坐标为(2cosα,sinα),利用P到直线l的距离公式得到表达式,然后求解最值.
解答 解:(1)$ρsin(θ-\frac{π}{3})=2$化简为$\sqrt{3}ρcosθ-ρsinθ+4=0$,
∴直线l的直角坐标方程为$\sqrt{3}x-y+4=0$; …(4分)
(12)设点P的坐标为(2cosα,sinα),
得P到直线l的距离$d=\frac{{|{2\sqrt{3}cosα-sinα+4}|}}{2}$,…(6分)
即$d=\frac{{|{\sqrt{13}cos({α+φ})+4}|}}{2}$,其中$cosφ=\frac{{2\sqrt{3}}}{{\sqrt{13}}},sinφ=\frac{1}{{\sqrt{13}}}$.
当sin(α+φ)=1时,${d_{max}}=\frac{1}{2}\sqrt{13}+2$. …(10分).
点评 本题考查极坐标与参数方程与直角坐标方程的互化,点到直线的距离公式的应用.考查计算能力.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 日 期 | 4月1日 | 4月7日 | 4月15日 | 4月21日 | 4月30日 |
| 温差x/℃ | 10 | 11 | 13 | 12 | 8 |
| 发芽数y/颗 | 23 | 25 | 30 | 26 | 16 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在五面体ABCDEF中,四边形ABCD为正方形,EF∥AD,平面ADEF⊥平面ABCD,且BC=2EF,AE=AF,点G是EF的中点.
如图,在五面体ABCDEF中,四边形ABCD为正方形,EF∥AD,平面ADEF⊥平面ABCD,且BC=2EF,AE=AF,点G是EF的中点.查看答案和解析>>
科目:高中数学 来源:2017届四川成都七中高三10月段测数学(理)试卷(解析版) 题型:填空题
设 为平面上过点
为平面上过点 的直线,
的直线, 的斜率等可能的取
的斜率等可能的取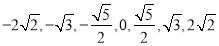 ,用
,用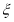 表示坐标原点到
表示坐标原点到 的距离,则随机变量
的距离,则随机变量 的数学期望
的数学期望 .
.
查看答案和解析>>
科目:高中数学 来源:2017届江西省红色七校高三上学期联考一数学(文)试卷(解析版) 题型:解答题
在 中,
中, 的对边分别是
的对边分别是 ,
, ,且
,且 .
.
(1)求证: 为等腰三角形;
为等腰三角形;
(2)若 的面积为
的面积为 ,且
,且 ,求
,求 边上的中线长.
边上的中线长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com