
| 日 期 | 4月1日 | 4月7日 | 4月15日 | 4月21日 | 4月30日 |
| 温差x/℃ | 10 | 11 | 13 | 12 | 8 |
| 发芽数y/颗 | 23 | 25 | 30 | 26 | 16 |
分析 (I)列出(m,n)的所有取值情况,设“m、n均不小于25”为事件A,找出事件A包含的基本事件个数,即可求解事件A的概率.
(II)求出y关于x的线性回归方程的相关数值即可.
(III)通过x=10时,x=8时,计算估计数据,然后判断线性回归方程是否可靠.
解答 解:(I)(m,n)的所有取值情况有
(23,25),(23,30),(23,26),(23,16),(25,30)(25,26),(25,16),(30,26),(30,16),(26,16),
共有10个,…(2分)
设“m、n均不小于25”为事件A,则事件A包含的基本事件有
(25,30),(25,26)(30,26),
∴$P(A)=\frac{3}{10}$,故事件A的概率为$\frac{3}{10}$;…(4分)
(II)由数据得$\overline x=12,\overline y=27$,$3\overline x\overline y=972$,$3{\overline x^2}=432$,
又$\sum_{i=1}^3{{x_i}{y_i}}=977$,$\sum_{i=1}^3{{x_i}^2}=434$,∴$\hat b=\frac{977-972}{434-432}=\frac{5}{2}$,$\hat a=27-\frac{5}{2}×12=-3$.
∴y关于x的线性回归方程为$\hat y=\frac{5}{2}x-3$;…(8分)
(III)当x=10时,$\hat y=22$,|22-23|<2,当x=8时,$\hat y=17$,|17-16|<2,
∴得到的线性回归方程是可靠的.…(12分)
点评 本题考查概率的求法,回归直线方程的求法,考查计算能力.


 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案科目:高中数学 来源: 题型:选择题
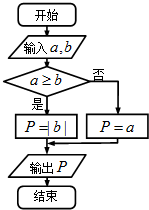 定义一种运算符号“→”,两个实数a,b的“a→b”运算原理如图所示,若函数f(x)=2→x,则f(2)+f(-2)=( )
定义一种运算符号“→”,两个实数a,b的“a→b”运算原理如图所示,若函数f(x)=2→x,则f(2)+f(-2)=( )| A. | -2 | B. | 0 | C. | 2 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 奇函数,且在(0,1)上是增函数,在(1,+∞)上是减函数 | |
| B. | 奇函数,且在(0,1)上是减函数,在(1,+∞)上是增函数 | |
| C. | 偶函数,且在(0,1)上是增函数,在(1,+∞)上是减函数 | |
| D. | 偶函数,且在(0,1)上是减函数,在(1,+∞)上是增函数 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源:2017届山东潍坊临朐县高三10月月考数学(文)试卷(解析版) 题型:选择题
将函数 图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),再把图象上所有的点向右平移1个单位,得到函数
图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),再把图象上所有的点向右平移1个单位,得到函数 的图象,则函数
的图象,则函数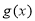 的单调递减区间是( )
的单调递减区间是( )
A. B.
B.
C.  D.
D.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com