练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    9．已知一个锥体的主视图和左视图如图所示，下列选项中，不可能是该锥体的俯视图的是（　　）
    A．B．C．D．

    分析 由三视图的作法规则，长对正，宽相等，对四个选项进行比对，找出错误选项．

    解答 解：本题中给出了正视图与左视图，故可以根据正视图与俯视图长对正，左视图与俯视图宽相等来找出正确选项
    A中的视图满足三视图的作法规则；
    B中的视图满足三视图的作法规则；
    C中的视图满足三视图的作法规则；
    D中的视图不满足锥体的顶点在右后方，故其为错误选项；
    故选：D．

    点评 本题考查三视图的作法，解题的关键是掌握住三视图的作法规则即长对正，宽相等，高平齐，利用这些规则即可选出正确选项．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

    2．设不等式组$\left\{\begin{array}{l}{y≤1}\\{x+y≥0}\\{x-y-2≤0}\end{array}\right.$ 表示的平面区域为D，在区域D内随机取一点M，则点M落在圆x2+y2=1内的概率为$\frac{π}{8}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    2．已知{an}为等比数列，若a1+a2+a3=2，a7+a8+a9=8，求a1+a2+a3+…+a3m-2+a3m-1+a3m=$\frac{2}{3}$（4m-1）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    18．陕西电视台为了了解观众对（央视快报）的满意度，通过都市热线随机调查观众，现从调查的观众中随机抽取12名，用精业图记录他们的满意度分数如图，则这12个分数的众数和中位数分别是（　　）
    A．92，92B．91，91C．92，91D．92，91，5

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    4．设直线l：y=kx+1经过抛物线x2=2py（p＞0）的焦点F，则p=2；已知Q，M分别是抛物线及其准线上的点，若$\overrightarrow{MQ}$=2$\overrightarrow{QF}$，则|MF|=4．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    13．定义一种运算符号“→”，两个实数a，b的“a→b”运算原理如图所示，若f（x）=（0→x）•x-（2→x），则y=f（x）在x∈[-2，2]时的最小值是（　　）
    A．-8B．$-\frac{1}{4}$C．-2D．-6

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    20．已知f（x）=|x-2|+x2，g（x）=x2-|x-a|+a（a∈R）．
    （Ⅰ）解不等式f（x）≤4；
    （Ⅱ）若不等式f（x）≥g（x）恒成立，求a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    17．某同学在生物研究性学习中，对春季昼夜温差大小与黄豆种子发芽多少之间的关系进行观测研究，于是他在4月份的30天中随机挑选了5天进行研究，且分别记录了每天昼夜温差与每天每100颗种子浸泡后的发芽数，得到如下资料：
    日  期4月1日4月7日4月15日4月21日4月30日
    温差x/℃101113128
    发芽数y/颗2325302616
    （Ⅰ）从这5天中任选2天，记发芽的种子数分别为m、n，求事件“m、n均不小于25”的概率；
    （Ⅱ）请根据4月7日、4月15日、4月21日三天的数据，求出y关于x的线性回归方程$\hat y=\hat bx+\hat a$；
    （Ⅲ）若由线性回归方程得到的估计数据与所选出的检验数据的误差均不超过2颗，则认为得到的线性回归方程是可靠的，若选取的是4月1日与4月30日的两组数据作为检验数据，试问（Ⅱ）中所得的线性回归方程是否可靠？
    参考公式：$\hat b=\frac{{\sum_{i=1}^n{{x_i}{y_i}-n\overline x\overline y}}}{{\sum_{i=1}^n{x_i^2-n{{\overline x}^2}}}}$，$\hat a=\overline y-\hat b\overline x$；
    参考数据：11×25+13×30+12×26=977，112+132+122=434．

    查看答案和解析>>

    科目：高中数学 来源：2017届四川成都七中高三10月段测数学（理）试卷（解析版） 题型：填空题

    设为平面上过点的直线，的斜率等可能的取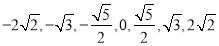，用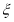表示坐标原点到的距离，则随机变量的数学期望 .

    查看答案和解析>>

    同步练习册答案