练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    18．陕西电视台为了了解观众对（央视快报）的满意度，通过都市热线随机调查观众，现从调查的观众中随机抽取12名，用精业图记录他们的满意度分数如图，则这12个分数的众数和中位数分别是（　　）
    A．92，92B．91，91C．92，91D．92，91，5

    分析 根据众数和中位数的概念，求出结果即可．

    解答 解：这组数据出现次数最多的是92，
    ∴众数是92；
    把这组数据按从小到大的顺序排列，排在第6、7位的是91、92，
    ∴中位数是$\frac{91+92}{2}$=91.5．
    故选：D．

    点评 本题考查了数据的中位数与众数的应用问题，是基础题目．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

    11．若f（x）=x2，?t∈R，对于?x∈[2，m]，都有f（x+t）≤2x成立，则m的最大值是8．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    10．已知数列{an}满足log3an+1=log3an+1（n∈N），且a2+a4+a6=9，则logb（a5+a7+a9）的值等于5．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    7．设f（x）是周期为4的周期函数，且当x∈（-1，3]时，$f（x）=\left\{{\begin{array}{l}{m\sqrt{1-{x^2}}，\;\;\;\;\;-1＜x≤1}\\{1-|{x-2}|，\;\;\;\;\;\;\;\;1＜x≤3}\end{array}}\right.$，若函数g（x）=3f（x）-x有且仅有五个零点，则正实数m的取值范围是（$\frac{\sqrt{15}}{3}$，$\sqrt{7}$）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    13．已知实数x，y满足$\left\{\begin{array}{l}{x≥1}\\{x-2y+1≤0}\\{x+y≤m}\end{array}\right.$，若此不等式组所表示的平面区域形状为三角形，则m的取值范围为（2，+∞），如果目标函数z=2x-y的最小值为-1，则实数m=4．

    查看答案和解析>>

    科目：高中数学 来源：2017届四川成都七中高三10月段测数学（文）试卷（解析版） 题型：选择题

    已知函数，在0处的导数为27，则（ ）

    A．-27 B．27 C．-3 D．3

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    9．已知一个锥体的主视图和左视图如图所示，下列选项中，不可能是该锥体的俯视图的是（　　）
    A．B．C．D．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

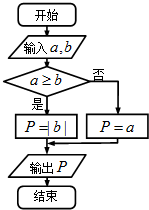    5．定义一种运算符号“→”，两个实数a，b的“a→b”运算原理如图所示，若函数f（x）=2→x，则f（2）+f（-2）=（　　）
    A．-2B．0C．2D．4

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    6．设y1=a3x+1，y2=a-2x（a＞0，且a≠1），当x为何值时，满足下列条件：
    （1）y1=y2；
    （2）y1＜y2．

    查看答案和解析>>

    同步练习册答案