
分析 设g(x)=f(x+t)-2x=x2+2(t-1)x+t2,由已知可得?x∈[2,m],g(x)≤0恒成立,即g(2)≤0且g(m)≤0,先求出t的范围,进而可得m的取值范围.
解答 解:设g(x)=f(x+t)-2x=x2+2(t-1)x+t2,
由题值?x∈[2,m],f(x+t)≤2x恒成立,
即?x∈[2,m],g(x)≤0恒成立,
即g(2)≤0且g(m)≤0,
即t2+4t≤0,m2+2(t-1)m+t2≤0,
则t∈[-4,0],
当t=0时,得到m2-2m≤0,解得0≤m≤2;
当t=-4时,得到m2-5m+4≤0,解得2≤m≤8
综上得到:m∈[2,8],
∴m的最大值是8,
故答案为:8.
点评 本题考查的知识点是函数恒成立问题,熟练掌握函数的图象和性质,会进行函数恒成立与不等式之间的转化是解答的关键,属于中档题.


 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源:2017届四川成都七中高三10月段测数学(文)试卷(解析版) 题型:选择题
已知在 中,
中, ,
, ,
, ,
, 是
是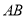 上的点,则
上的点,则 到
到 的距离的乘积的最大值为( )
的距离的乘积的最大值为( )
A.3 B.2 C. D.9
D.9
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=lnx | B. | y=x3 | C. | $y={(\frac{1}{2})^x}$ | D. | y=sinx |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 陕西电视台为了了解观众对(央视快报)的满意度,通过都市热线随机调查观众,现从调查的观众中随机抽取12名,用精业图记录他们的满意度分数如图,则这12个分数的众数和中位数分别是( )
陕西电视台为了了解观众对(央视快报)的满意度,通过都市热线随机调查观众,现从调查的观众中随机抽取12名,用精业图记录他们的满意度分数如图,则这12个分数的众数和中位数分别是( )| A. | 92,92 | B. | 91,91 | C. | 92,91 | D. | 92,91,5 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com