
| A. | 2 | B. | 3 | C. | 0 | D. | 1 |
分析 注意到绝对值,分x<0与x≥0讨论,从而函数的单调性及函数零点的判定定理判断零点的个数.
解答 解:当x<0时,
f(x)=x•2|x|-x-1=x(2|x|-1)-1<-1;
故函数f(x)=x•2|x|-x-1在(-∞,0)上没有零点;
当x≥0时,
f(x)=x•2x-x-1
f′(x)=2x+xln2•2x-1
=xln2•2x+2x-1≥0;
故f(x)=x•2x-x-1在[0,+∞)上是增函数,
且f(0)=-1,f(2)=8-2-1=5>0;
故函数f(x)=x•2|x|-x-1在[0,+∞)上有且只有一个零点;
综上所述,函数f(x)=x•2|x|-x-1的零点个数为1;
故选:D.
点评 本题考查了函数的单调性的判断及函数零点的判定定理的应用,属于基础题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 奇函数,且在(0,1)上是增函数,在(1,+∞)上是减函数 | |
| B. | 奇函数,且在(0,1)上是减函数,在(1,+∞)上是增函数 | |
| C. | 偶函数,且在(0,1)上是增函数,在(1,+∞)上是减函数 | |
| D. | 偶函数,且在(0,1)上是减函数,在(1,+∞)上是增函数 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x1>x2 | B. | x1<x2 | C. | x12<x22 | D. | |x1|>|x2| |
查看答案和解析>>
科目:高中数学 来源:2017届四川成都七中高三10月段测数学(理)试卷(解析版) 题型:解答题
已知椭圆 的离心率为
的离心率为 ,以
,以 为圆心,椭圆的短半轴长为半径的圆与直线
为圆心,椭圆的短半轴长为半径的圆与直线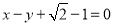 相切.
相切.
(1)求椭圆 的标准方程;
的标准方程;
(2)已知点 ,和面内一点
,和面内一点 ,过点
,过点 任作直线
任作直线 与椭圆
与椭圆 相交于
相交于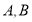 两点,设直线
两点,设直线 的斜率分别为
的斜率分别为 ,若
,若 ,试求
,试求 满足的关系式.
满足的关系式.
查看答案和解析>>
科目:高中数学 来源:2017届四川成都七中高三10月段测数学(理)试卷(解析版) 题型:选择题
设曲线 及直线
及直线 所围成的封闭图形为区域
所围成的封闭图形为区域 ,不等式组
,不等式组 所确定的区域为
所确定的区域为 ,在区域
,在区域 内随机取一点,该点恰好在区域
内随机取一点,该点恰好在区域 的概率为( )
的概率为( )
A. B.
B. C.
C. D.
D.
查看答案和解析>>
科目:高中数学 来源:2017届江西省红色七校高三上学期联考一数学(文)试卷(解析版) 题型:选择题
“序数”指每个数字比其左边的数字大的自然数(如1258),在两位的“序数”中任取一个数比56大的概率是( )
A. B.
B. C.
C. D.
D.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com