练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    14．已知|x-4|+|3-x|＜a，x∈∅，求a的取值范围．

    分析 利用绝对值不等式求解最小值，即可推出a的范围．

    解答 解：|x-4|+|3-x|≥|x-4+3-x|=1，
    |x-4|+|3-x|＜a，x∈∅，
    可得a≤1．
    a的取值范围：（-∞，1]．

    点评 本题考查绝对值不等式的解法，绝对值的几何意义，考查分析问题解决问题的能力．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

    7．设f（x）是周期为4的周期函数，且当x∈（-1，3]时，$f（x）=\left\{{\begin{array}{l}{m\sqrt{1-{x^2}}，\;\;\;\;\;-1＜x≤1}\\{1-|{x-2}|，\;\;\;\;\;\;\;\;1＜x≤3}\end{array}}\right.$，若函数g（x）=3f（x）-x有且仅有五个零点，则正实数m的取值范围是（$\frac{\sqrt{15}}{3}$，$\sqrt{7}$）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

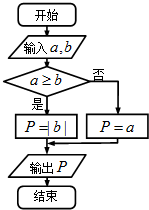    5．定义一种运算符号“→”，两个实数a，b的“a→b”运算原理如图所示，若函数f（x）=2→x，则f（2）+f（-2）=（　　）
    A．-2B．0C．2D．4

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    2．在区间[-2，1]上随机取一个实数x，则x使不等式|x-1|≤1成立的概率为$\frac{1}{3}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    9．在平面直角坐标系xOy中，已知曲线C的参数方程为$\left\{\begin{array}{l}x=2cosα\\ y=sinα\end{array}\right.（{α为参数}）$．以直角坐标系原点O为极点，x轴的正半轴为极轴建立极坐标系，直线l的极坐标方程为$ρsin（{θ-\frac{π}{3}}）=2$．
    （1）求直线l的直角坐标方程；
    （2）点P为曲线C上的动点，求点P到直线l距离的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    19．当a为何值时，不等式（a2-1）x2-（a-1）x-1＜0的解集为R．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    6．设y1=a3x+1，y2=a-2x（a＞0，且a≠1），当x为何值时，满足下列条件：
    （1）y1=y2；
    （2）y1＜y2．

    查看答案和解析>>

    科目：高中数学 来源：2017届四川成都七中高三10月段测数学（理）试卷（解析版） 题型：选择题

    如果某射手每次射击击中目标的概率为0.74，每次射击的结果相互独立，那么他在10次射击中，最有可能击中目标儿几次（ ）

    A．6 B．7 C．8 D．9

    查看答案和解析>>

    科目：高中数学 来源：2017届江西省红色七校高三上学期联考一数学（文）试卷（解析版） 题型：选择题

    已知函数，若对任意都有成立，则（ ）

    A. B. C. D.

    查看答案和解析>>

    同步练习册答案