
设数列 为等差数列,且
为等差数列,且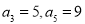 ;数列
;数列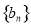 的前n项和为
的前n项和为 .
.
(1)求数列 ,
,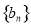 的通项公式;
的通项公式;
(2)若 为数学
为数学 的前n项和,求
的前n项和,求 .
.
(1)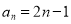 ,
,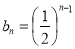 ;(2)
;(2)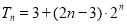 .
.
【解析】
试题分析:(1)给出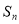 与
与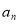 的关系,求
的关系,求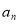 ,常用思路:一是利用
,常用思路:一是利用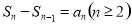 转化为
转化为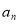 的递推关系,再求其通项公式;二是转化为
的递推关系,再求其通项公式;二是转化为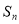 的递推关系,先求出
的递推关系,先求出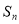 与
与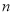 的关系,再求
的关系,再求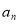 ;(2)等差数列基本量的求解是等差数列的一类基本问题,解决这类问题的关键在于熟练掌握等差数列的有关公式并能灵活运用;(3)一般地,如果数列
;(2)等差数列基本量的求解是等差数列的一类基本问题,解决这类问题的关键在于熟练掌握等差数列的有关公式并能灵活运用;(3)一般地,如果数列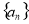 是等差数列,
是等差数列,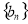 是等比数列,求数列
是等比数列,求数列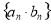 的前
的前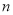 项的和时,可采用错位相减法求和,一般是和式两边同乘以等比数列
项的和时,可采用错位相减法求和,一般是和式两边同乘以等比数列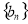 的公比,然后做差求解.
的公比,然后做差求解.
试题解析:解(1)数列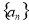 为等差数列,所以
为等差数列,所以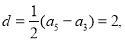 又因为
又因为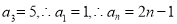
由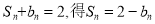
n=1时,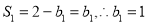
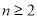 时,
时,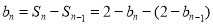
所以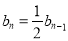 4分
4分
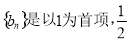 为公比的等比数列
为公比的等比数列

 6分
6分
(2)由(1)知,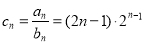 7分
7分
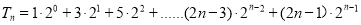
 9分
9分
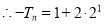 +
+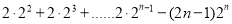
=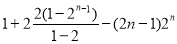
=1-4+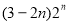 11分
11分
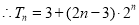 . 12分
. 12分
考点:1、求等差数列、等比数列的通项公式;2、错位相减求数列的和.


科目:高中数学 来源: 题型:
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
| A、P1,P3 |
| B、P1,P4 |
| C、P2,P3 |
| D、P2,P4 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| (a1+a2+…+an)π |
| 3 |
| A、z<y<x |
| B、x<z<y |
| C、x<y<z |
| D、y<z<x |
查看答案和解析>>
科目:高中数学 来源:2015届四川省泸州市高三上学期第一次诊断性考试理科数学试卷(解析版) 题型:解答题
(本小题满分12分) 已知函数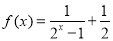 .
.
(1)判断函数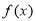 的奇偶性,并证明;
的奇偶性,并证明;
(2)若对于任意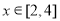 ,不等式
,不等式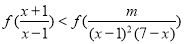 恒成立,求正实数
恒成立,求正实数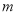 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源:2015届山东省高三第一次诊断性考试理科数学试卷(解析版) 题型:选择题
某人随机地在如图所示正三角形及其外接圆区域内部投针(不包括三角形边界及圆的边界),则针扎到阴影区域(不包括边界)的概率为
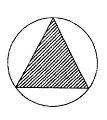
A.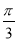 B.
B.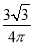 C.
C.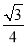 D.以上全错
D.以上全错
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com