
| (a1+a2+…+an)π |
| 3 |
| A、z<y<x |
| B、x<z<y |
| C、x<y<z |
| D、y<z<x |
| (a1+a2+…+an)π |
| 3 |
| 50π |
| 3 |
| 2π |
| 3 |
| 2π |
| 3 |
| ||
| 2 |
| 2π |
| 3 |
| 1 |
| 2 |
| 2π |
| 3 |
| 3 |


 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案科目:高中数学 来源: 题型:
| A、4025 |
| B、4026 |
| C、22013 |
| D、22014 |
查看答案和解析>>
科目:高中数学 来源:2015届四川省绵阳市高三一诊测试文科数学试卷(解析版) 题型:选择题
设各项均不为0的数列{an}满足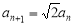 (n≥1),若
(n≥1),若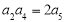 ,则a3=( )
,则a3=( )
(A)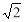 (B)2
(B)2
(C)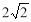 (D)4
(D)4
查看答案和解析>>
科目:高中数学 来源:2015届四川省泸州市高三上学期第一次诊断性考试文科数学试卷(解析版) 题型:选择题
已知命题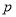 :
: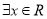 ,
,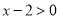 ,命题
,命题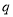 :
: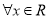 ,
,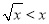 ,则下列说法中正确的是( )
,则下列说法中正确的是( )
A、命题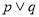 是假命题 B、命题
是假命题 B、命题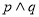 是真命题
是真命题
C、命题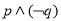 是真命题 D、命题
是真命题 D、命题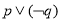 是假命题
是假命题
查看答案和解析>>
科目:高中数学 来源:2015届山东省高三第一次诊断性考试理科数学试卷(解析版) 题型:解答题
设数列 为等差数列,且
为等差数列,且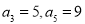 ;数列
;数列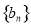 的前n项和为
的前n项和为 .
.
(1)求数列 ,
,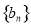 的通项公式;
的通项公式;
(2)若 为数学
为数学 的前n项和,求
的前n项和,求 .
.
查看答案和解析>>
科目:高中数学 来源:2015届山东省高三第一次诊断性考试文科数学试卷(解析版) 题型:解答题
已知向量 ,函数
,函数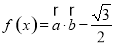 的最小正周期为
的最小正周期为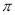 .
.
(1)求函数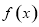 的单调增区间;
的单调增区间;
(2)如果△ABC的三边 所对的角分别为
所对的角分别为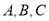 ,且满足
,且满足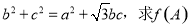 的值.
的值.
查看答案和解析>>
科目:高中数学 来源:2015届山东师范大学附属中学高三第一次模拟考试文科数学试卷(解析版) 题型:解答题
如图所示,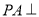 平面ABCD,四边形ABCD为正方形,且
平面ABCD,四边形ABCD为正方形,且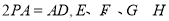 分别是线段PA、PD、CD、BC的中点.
分别是线段PA、PD、CD、BC的中点.
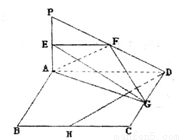
(1)求证:BC//平面EFG;
(2)求证: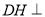 平面AEG;
平面AEG;
(3)求三棱锥E-AFG与四棱锥P-ABCD的体积比.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com