
 如图所示,为测量山高MN,选择A和另一座山的山顶C为测量观测点,从A测得M点的仰角∠MAN=60°,C点的仰角∠CAB=30°,以及∠MAC=105°,从C测得∠MCA=45°,已知山高BC=150米,则所求山高MN为150$\sqrt{6}$m.
如图所示,为测量山高MN,选择A和另一座山的山顶C为测量观测点,从A测得M点的仰角∠MAN=60°,C点的仰角∠CAB=30°,以及∠MAC=105°,从C测得∠MCA=45°,已知山高BC=150米,则所求山高MN为150$\sqrt{6}$m. 分析 由题意,通过解△ABC可先求出AC的值,解△AMC,由正弦定理可求AM的值,在RT△MNA中,AM=300$\sqrt{2}$m,∠MAN=60°,从而可求得MN的值.
解答 解:在RT△ABC中,∠CAB=30°,BC=150m,所以AC=300m.
在△AMC中,∠MAC=105°,∠MCA=45°,从而∠AMC=30°,
由正弦定理得,AM=$\frac{ACsin45°}{sin30°}$=300$\sqrt{2}$m.
在RT△MNA中,AM=300$\sqrt{2}$m,∠MAN=60°,
得MN=300$\sqrt{2}$×$\frac{\sqrt{3}}{2}$=150$\sqrt{6}$m.
故答案为150$\sqrt{6}$m.
点评 本题主要考察了正弦定理的应用,考察了解三角形的实际应用,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | 至少选一个海滨城市 | B. | 恰好选一个海滨城市 | ||
| C. | 至多选一个海滨城市 | D. | 两个都选海滨城市 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题

查看答案和解析>>
科目:高中数学 来源: 题型:解答题
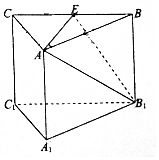 如图,在直棱柱ABC-A1B1C1中,AB=AC=4,∠BAC=90°,E为BC的中点.
如图,在直棱柱ABC-A1B1C1中,AB=AC=4,∠BAC=90°,E为BC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 8 | B. | 4 | C. | 2 | D. | 1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com