

分析 可以看到第三行起每一行空心圆点的个数都是前两行空心圆点个数的和,由此可以得到一个递推关系,利用此递推关系求解即可.
解答 解:由题意及图形知不妨构造这样一个数列{an}表示空间心圆点的个数变化规律,令a1=1,a2=0,n≥3时,an=an-1+an-2,本数列中的n对应着图形中的第n行中空心圆点的个数.由此知a10即所求.
故各行中空心圆点的个数依次为1,0,1,1,2,3,5,8,13,21,34,55,89,..
a10=21,即第10行中空心圆点的个数是21
故答案为:21.
点评 本题主要考查了数列的应用,解题的关键构造这样一个数列{an}表示空间心圆点的个数变化规律,令a1=1,a2=0,n≥3时,an=an-1+an-2,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{3}$ | B. | 3 | C. | $2\sqrt{3}$ | D. | 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -2 | B. | -2i | C. | 2 | D. | 2i |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
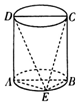
| A. | AE⊥CE | B. | BE⊥DE | C. | DE⊥CE | D. | 面ADE⊥面BCE |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 如图所示,为测量山高MN,选择A和另一座山的山顶C为测量观测点,从A测得M点的仰角∠MAN=60°,C点的仰角∠CAB=30°,以及∠MAC=105°,从C测得∠MCA=45°,已知山高BC=150米,则所求山高MN为150$\sqrt{6}$m.
如图所示,为测量山高MN,选择A和另一座山的山顶C为测量观测点,从A测得M点的仰角∠MAN=60°,C点的仰角∠CAB=30°,以及∠MAC=105°,从C测得∠MCA=45°,已知山高BC=150米,则所求山高MN为150$\sqrt{6}$m.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充要条件 | B. | 充分不必要条件 | ||
| C. | 必要不充分条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,-6) | B. | (-∞,-6)∪(6,+∞) | C. | (6,+∞) | D. | (-6,6) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com