练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    如图，圆锥顶点为p．底面圆心为o，其母线与底面所成的角为22.5°．AB和CD是底面圆O上的两条平行的弦，轴OP与平面PCD所成的角为60°

    (Ⅰ)证明：平面PAB与平面PCD的交线平行于底面；

    (Ⅱ)求cos∠COD．

    答案：
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    圆锥曲线上任意两点连成的线段称为弦．若圆锥曲线上的一条弦垂直于其对称轴，我们将该弦称之为曲线的垂轴弦．已知点P（
    x0，y0）、M（m，n）是圆锥曲线C上不与顶点重合的任意两点，MN是垂直于x轴的一条垂轴弦，直线MP，NP分别交x轴于点E（xE，0）和点F（xF，0）．
    （Ⅰ）试用x0，y0，m，n的代数式分别表示xE和xF；
    （Ⅱ）已知“若点P（x0，y0）是圆C：x2+y2=R2上的任意一点（
    x0•y0≠0），MN是垂直于x轴的垂轴弦，直线MP、NP分别交x轴于点E（xE，0）和点F（xF，0），则xE•xF=R2”．类比这一结论，我们猜想：“若曲线C的方程为
    x2
    a2
    +
    y2
    b2
    =1(a＞b＞0)    （如图），则xE•xF也是与点M、N、P位置无关的定值”，请你对该猜想给出证明．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

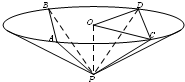    （2013•安徽）如图，圆锥顶点为P，底面圆心为O，其母线与底面所成的角为22.5°，AB和CD是底面圆O上的两条平行的弦，轴OP与平面PCD所成的角为60°，
    （1）证明：平面PAB与平面PCD的交线平行于底面；
    （2）求cos∠COD．

    查看答案和解析>>

    科目：高中数学 来源：高三数学教学与测试 题型：044

    已知球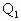的半径为R，内切于顶点为P的圆锥(轴截面如图)．设∠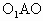＝θ．

    　　

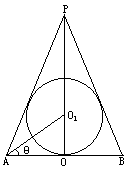
    (1)试用R，θ表示圆锥底面半径r，母线l和全面积S；

    (2)当θ为何值时，圆锥全面积取最小值？最小值是多少？

    查看答案和解析>>

    科目：高中数学 来源：2013年安徽省高考数学试卷（理科）（解析版） 题型：解答题

    如图，圆锥顶点为P，底面圆心为O，其母线与底面所成的角为22.5°，AB和CD是底面圆O上的两条平行的弦，轴OP与平面PCD所成的角为60°，
    （1）证明：平面PAB与平面PCD的交线平行于底面；
    （2）求cos∠COD．

    查看答案和解析>>

    同步练习册答案