
从双曲线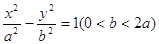 的左焦点
的左焦点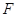 引圆
引圆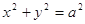 的切线,切点为T, 延长FT交双曲线右支于点P, O为坐标原点,M为PF 的中点,则
的切线,切点为T, 延长FT交双曲线右支于点P, O为坐标原点,M为PF 的中点,则 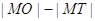 与
与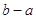 的大小关系为
的大小关系为 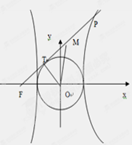
A.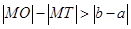 |
B.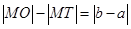 |
C.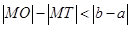 |
| D.不能确定 |
B
解析试题分析:将点P置于第一象限.设F1是双曲线的右焦点,连接PF1.∵M、O分别为FP、FF1的中点,∴|MO|=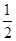 |PF1|.又由双曲线定义得, |PF|-|PF1|=2a, |FT|==b.故|MO|-|MT|=
|PF1|.又由双曲线定义得, |PF|-|PF1|=2a, |FT|==b.故|MO|-|MT|=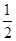 |PF1|-|MF|+|FT|=
|PF1|-|MF|+|FT|=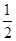 (|PF1|-|PF|)+|FT|
(|PF1|-|PF|)+|FT|
=b-a.故选B.
考点:本题主要考查了直线与圆锥曲线的综合应用能力,具体涉及到轨迹方程的求法及直线与双曲线的相关知识,解题时要注意合理地进行等价转化.
点评:解决该试题的关键是将点P置于第一象限.设F1是双曲线的右焦点,连接PF1.由M、O分别为FP、FF1的中点,知|MO|= 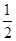 |PF1|.由双曲线定义,知|PF|-|PF1|=2a,|FT|=b.由此知|MO|-|MT|=
|PF1|.由双曲线定义,知|PF|-|PF1|=2a,|FT|=b.由此知|MO|-|MT|=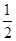 (|PF1|-|PF|)+|FT|=b-a.
(|PF1|-|PF|)+|FT|=b-a.


湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com