
【题目】某市在对学生的综合素质评价中,将其测评结果分为“优秀、合格、不合格”三个等级,其中不小于80分为“优秀”,小于60分为“不合格”,其它为“合格”.
(1)某校高二年级有男生500人,女生400人,为了解性别对该综合素质评价结果的影响,采用分层抽样的方法从高二学生中抽取了90名学生的综合素质评价结果,其各个等级的频数统计如表:
等级 | 优秀 | 合格 | 不合格 |
男生(人) | 30 | x | 8 |
女生(人) | 30 | 6 | y |
根据表中统计的数据填写下面2×2列联表,并判断是否有90%的把握认为“综合素质评价测评结果为优秀与性别有关”?
男生 | 女生 | 总计 | |
优秀 | |||
非优秀 | |||
总计 |
临界值表:
0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 | |
k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(2)以(1)中抽取的90名学生的综合素质评价等级的频率作为全市各个评价等级发生的概率,且每名学生是否“优秀”相互独立,现从该市高二学生中随机抽取4人.
(i)求所选4人中恰有3人综合素质评价为“优秀”的概率;
(ii)记X表示这4人中综合素质评价等级为“优秀”的人数,求X的数学期望.
附:参考数据与公式
参考公式:K2= ![]() ,其中n=a+b+c+d.
,其中n=a+b+c+d.
【答案】
(1)解:设从高二年级男生中抽出m人,则 ![]() ,
,
解得m=50.
∴x=50﹣38=12,y=40﹣36=4.
∴2×2列联表为:
男生 | 女生 | 总计 | |
优秀 | 30 | 30 | 60 |
非优秀 | 20 | 10 | 30 |
总计 | 50 | 40 | 90 |
∴K2= ![]() =2.25<2.706,
=2.25<2.706,
∴没有90%的把握认为“综合素质评价测评结果为优秀与性别有关”.
(2)解:(i)由(1)知等级为“优秀”的学生的频率为 ![]() ,
,
∴从该市高二学生中随机抽取一名学生,该生为“优秀”的概率为 ![]() .
.
记“所选4名学生中恰有3人综合素质评价为‘优秀’学生”为事件A,
则事件A发生的概率为:P(A)= ![]() =
= ![]() .
.
(ii)X表示这4个人中综合速度评价等级为“优秀”的个数,
由题意,随机变量X~B(4, ![]() ),
),
∴X的数学期望E(X)=4× ![]() =
= ![]()
【解析】(1)先求出从高一年级男生中抽出人数及x,y,作出2×2列联表,求出K2=1.125<2.706,从而得到没有90%的把握认为“综合素质评价测评结果为优秀与性别有关”.(2)(i)由(1)知等级为“优秀”的学生的频率为 ![]() ,从该市高二学生中随机抽取一名学生,该生为“优秀”的概率为
,从该市高二学生中随机抽取一名学生,该生为“优秀”的概率为 ![]() .由此能求出所选4名学生中恰有3人综合素质评价为‘优秀’学生的概率.(ii)X表示这4个人中综合速度评价等级为“优秀”的个数,由题意,随机变量X~B(4,
.由此能求出所选4名学生中恰有3人综合素质评价为‘优秀’学生的概率.(ii)X表示这4个人中综合速度评价等级为“优秀”的个数,由题意,随机变量X~B(4, ![]() ),由此能求出X的数学期望.
),由此能求出X的数学期望.


科目:高中数学 来源: 题型:
【题目】已知函数![]() ,求解下列问题(1)求函数f(x)的定义域;(2)求f(﹣1),f(12)的值;.
,求解下列问题(1)求函数f(x)的定义域;(2)求f(﹣1),f(12)的值;.
(1)求函数f(x)的定义域;
(2)求f(﹣1),f(12)的值;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于集合A={x|x=m2﹣n2 , m∈Z,n∈Z},因为16=52﹣32 , 所以16∈A,研究下列问题:
(1)1,2,3,4,5,6六个数中,哪些属于A,哪些不属于A,为什么?
(2)讨论集合B={2,4,6,8,…,2n,…}中有哪些元素属于A,试给出一个普通的结论,不必证明.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线l: 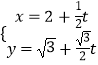 (t为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C的极坐标方程为ρ=2.
(t为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C的极坐标方程为ρ=2.
(1)若点M的直角坐标为(2, ![]() ),直线l与曲线C交于A、B两点,求|MA|+|MB|的值;
),直线l与曲线C交于A、B两点,求|MA|+|MB|的值;
(2)设曲线C经过伸缩变换 ![]() 得到曲线C′,求曲线C′的内接矩形周长的最大值.
得到曲线C′,求曲线C′的内接矩形周长的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示的分数三角形,称为“莱布尼茨三角形”.这个三角形的规律是:各行中的每一个数,都等于后面一行中与它相邻的两个数之和(例如第4行第2个数 ![]() 等于第5行中的第2个数
等于第5行中的第2个数 ![]() 与第3个数
与第3个数 ![]() 之和).则
之和).则
在“莱布尼茨三角形”中,第10行从左到右第2个数到第8个数中各数的倒数之和为( )
A.5010
B.5020
C.10120
D.10130
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】利民奶牛场在2016年年初开始改进奶牛饲养方法,同时每月增加一定数目的产奶奶牛,2016年2到5月该奶牛场的产奶量如表所示:
月份 | 2 | 3 | 4 | 5 |
产奶量y(吨) | 2.5 | 3 | 4 | 4.5 |
(1)在给定的坐标系中画出表中数据的散点图; 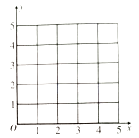
(2)求出y关于x的线性回归方程;
(3)试预测该奶牛场6月份的产奶量? (注:回归方程 ![]() =
= ![]() x+
x+ ![]() 中,
中, ![]() =
= 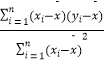 =
= 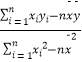 ,
, ![]() =
= ![]() ﹣
﹣ ![]()
![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】袋中共有15个除了颜色外完全相同的球,其中有10个白球,5个红球.从袋中任取2个球,所取的2个球中恰有1个白球,1个红球的概率为( )
A.![]()
B.![]()
C.![]()
D.1
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在三棱锥S﹣ABC中,△ABC是边长为2 ![]() 的正三角形,平面SAC⊥平面ABC,SA=SC=2,M、N分别为AB、SB的中点.
的正三角形,平面SAC⊥平面ABC,SA=SC=2,M、N分别为AB、SB的中点. 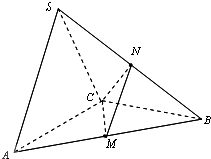
(1)证明:AC⊥SB;
(2)求三棱锥B﹣CMN的体积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com