
分析 根据题意,三棱锥S-ABC扩展为正方体,正方体的外接球的球心就是正方体体对角线的中点,求出正方体的对角线的长度,即可求解球的半径,从而可求三棱锥S-ABC的外接球的表面积.
解答 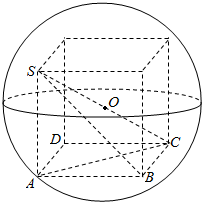 解:三棱锥S-ABC的所有顶点都在球O的表面上,SA⊥平面ABC,AB⊥BC,又SA=AB=BC=2,
解:三棱锥S-ABC的所有顶点都在球O的表面上,SA⊥平面ABC,AB⊥BC,又SA=AB=BC=2,
三棱锥扩展为正方体的外接球,外接球的直径就是正方体的对角线的长度,
∴球的半径R=$\frac{1}{2}\sqrt{2+2+2}$=$\frac{\sqrt{6}}{2}$.
球的表面积为:4πR2=4π•($\frac{\sqrt{6}}{2}$)2=6π.
故答案为:6π.
点评 本题考查三棱锥S-ABC的外接球的表面积,解题的关键是确定三棱锥S-ABC的外接球的球心与半径.


 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案科目:高中数学 来源: 题型:选择题
| A. | c>a>b | B. | c>b>a | C. | a>c>b | D. | a>b>c |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
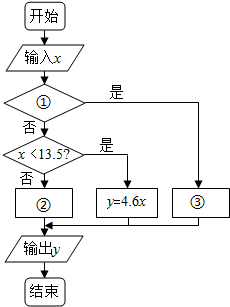 为了鼓励市民节约用水,太原市对已实施“一户一表、水表出户”的居民生活用水的收费标准规定如下:一级水量每户每月9立方米及以下,每立方米销售价格为2.30元;二级水量每户每月9立方米以上至13.5立方米,每立方米销售价格为4.60元;三级水量每户每月13.5立方米及以上,每立方米销售价格为6.90元,
为了鼓励市民节约用水,太原市对已实施“一户一表、水表出户”的居民生活用水的收费标准规定如下:一级水量每户每月9立方米及以下,每立方米销售价格为2.30元;二级水量每户每月9立方米以上至13.5立方米,每立方米销售价格为4.60元;三级水量每户每月13.5立方米及以上,每立方米销售价格为6.90元,查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com