Question

4．为了鼓励市民节约用水，太原市对已实施“一户一表、水表出户”的居民生活用水的收费标准规定如下：一级水量每户每月9立方米及以下，每立方米销售价格为2.30元；二级水量每户每月9立方米以上至13.5立方米，每立方米销售价格为4.60元；三级水量每户每月13.5立方米及以上，每立方米销售价格为6.90元，
（1）写出太原市居民每户每月生活用水费用y（单位：元）与其用水量J（单位：立方米）之间的关系式；
（2）如图是按上述规定计算太原市居民每户每月生活用水费用的程序框图，但步骤没有全部给出，请将其补充完整（将答案写在下列横线上）．
①x≤9②y=6.9x③y=2.3x．

Answer 1

分析 （1）由题意可知所求函数应为分段函数，根据题意即可列出函数关系式；
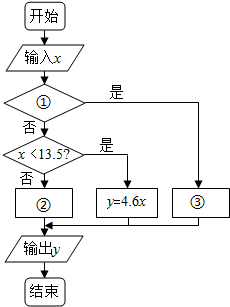
（2）程序框图为条件结构，根据①的条件选择“是““否“两个分支进行执行，结合分段函数的解析式即可得解．

解答 （本题满分为8分）
解：（1）由题意可知所求函数应为分段函数，根据题意可得：
y=$\left\{\begin{array}{l}{\stackrel{2.3x}{4.6x}}&{\stackrel{0≤x≤9}{9＜x＜13.5}}\\{6.9x}&{x≥13.5}\end{array}\right.$…4分
（2）①x≤9，②y=6.9x，③y=2.3x．
故答案为：x≤9，y=6.9x，y=2.3x…8分

点评 本题考查的重点是分段函数，考查了选择结构，考查的是函数与生活实际结合的问题，解题的关键是列出分段函数表达式，属于基础题．