
���� �ɹ�Բx2+y2=r2��һ������߷���x0x+y0y=r2�����Dz�������ƶϳ�����Բ��һ������߷��̣���x0x��x2����y0y��y2�����ɵã�
��� �⣺��ȹ�Բ��һ������߷��̣��ɺ���������
����Բ��һ��M��x0��y0���������߷���Ϊ$\frac{{x}_{0}x}{{a}^{2}}+\frac{{y}_{0}y}{{b}^{2}}=1$��
�ʴ�Ϊ��$\frac{{x}_{0}x}{{a}^{2}}+\frac{{y}_{0}y}{{b}^{2}}=1$��
���� ���⿼��������������õ����ۣ�����ʱҪ����۲죬ע�����������������֤���������������ڻ����⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | -13 | B�� | -7 | C�� | 7 | D�� | 13 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{3}{2}$ | B�� | $\sqrt{2}$+$\frac{1}{2}$ | C�� | 2 | D�� | $\sqrt{2}$+1 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
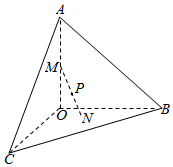 ��֪����A-BCO��OA��OB��OC������ֱ�ҳ��Ⱦ�Ϊ4����Ϊ2���߶�MN��һ���˵�M����OA���˶�����һ���˵�N�ڡ�BCO���˶������߽磩����MN���е�P�Ĺ켣������������Χ�ɵļ���������Ϊ$\frac{��}{6}$��$\frac{32}{3}$-$\frac{��}{6}$��
��֪����A-BCO��OA��OB��OC������ֱ�ҳ��Ⱦ�Ϊ4����Ϊ2���߶�MN��һ���˵�M����OA���˶�����һ���˵�N�ڡ�BCO���˶������߽磩����MN���е�P�Ĺ켣������������Χ�ɵļ���������Ϊ$\frac{��}{6}$��$\frac{32}{3}$-$\frac{��}{6}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | -log20122011 | B�� | -1 | C�� | ��log20122011��-1 | D�� | 1 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com