
如右图.M是棱长为2cm的正方体ABCD-A1B1C1D1的棱CC1的中点,沿正方体表面从点A到点M的最短路程是 cm.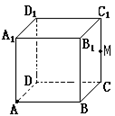
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案科目:高中数学 来源: 题型:填空题
如图,已知DE⊥平面ACD,DE//AB,△ACD是正三角形,AD=DE=2AB,且F是CD的中点。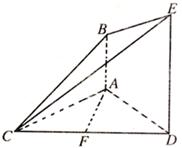
(I)求证:AF//平面BCE;
(II)求证:平面BCE⊥平面CDE;
(III)求平面BCE与平面ACD所成锐二面角的大小。
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
对于四面体ABCD,以下命题中,真命题的序号为 (填上所有真命题的序号)
①若AB=AC,BD=CD,E为BC中点,则平面AED⊥平面ABC;
②若AB⊥CD,BC⊥AD,则BD⊥AC;
③若所有棱长都相等,则该四面体的外接球与内切球的半径之比为2:1;
④若以A为端点的三条棱所在直线两两垂直,则A在平面BCD内的射影为△BCD的垂心;
⑤分别作两组相对棱中点的连线,则所得的两条直线异面。
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
下列命题中正确的是 (填上你认为所有正确的选项)
①空间中三个平面 ,若
,若 ,则
,则 ∥
∥
②空间中两个平面 ,若
,若 ∥
∥ ,直线
,直线 与
与 所成角等于直线
所成角等于直线 与
与 所成角, 则
所成角, 则 ∥
∥ .
.
③球 与棱长为
与棱长为 正四面体各面都相切,则该球的表面积为
正四面体各面都相切,则该球的表面积为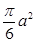 ;
;
④三棱锥 中,
中, 则
则 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com