
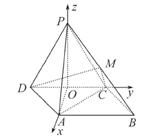
如图,四棱锥P-ABCD中,侧面PDC是边长为2的正三角形,且与底面垂直,底面ABCD是菱形且∠ADC=60°,M为PB的中点.
(1)求PA与底面ABCD所成角的大小.
(2)求证:PA⊥平面CDM.
(3)求二面角D-MC-B的余弦值.

解:(1)取DC的中点O,由△PDC是正三角形,有PO⊥DC.
又∵平面PDC⊥底面ABCD,∴PO⊥平面ABCD于O.
连接OA,则OA是PA在底面上的射影,
∴∠PAO就是PA与底面ABCD所成的角.
∵∠ADC=60°,由已知△PCD和△ACD是全等的正三角形,从而求得OA=OP= .
.
∴∠PAO=45°,∴PA与底面ABCD所成角的大小为45°. ……………4分
(2)由底面ABCD为菱形且∠ADC=60°,DC=2,DO=1,得OA⊥DC.
建立空间直角坐标系如图,
 则A(
则A( ,0,0),P(0,0,
,0,0),P(0,0, ),D(0,-1,0),B(
),D(0,-1,0),B( ,2,0),C(0,1,0).
,2,0),C(0,1,0).
由M为PB中点,∴M(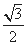 ,1,
,1,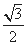 ),
),
∴ =(
=(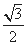 ,2,
,2,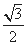 ),
),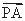 =(
=( ,0,-
,0,- ),
), =(0,2,0),
=(0,2,0),
∴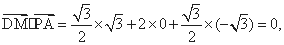
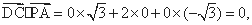
∴PA⊥DM,PA⊥DC.又DM∩DC=D,∴PA⊥平面CDM. ……………8分
(3)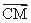 =(
=(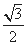 ,0,
,0,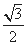 ),
), =(
=( ,1,0).
,1,0).
设平面BMC的法向量n=(x,y,z),
则n·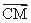 =0,从而x+z=0;①
=0,从而x+z=0;①
n· =0,从而
=0,从而 x+y=0,②
x+y=0,②
由①②,取x=-1,则y= ,z=1.∴可取n=(-1,
,z=1.∴可取n=(-1, ,1).
,1).
由(2)知平面CDM的法向量可取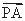 =(
=( ,0,-
,0,- ),
),
∴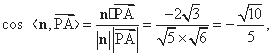
∴所求二面角的余弦值为 . ……………12分
. ……………12分


 英才点津系列答案
英才点津系列答案 红果子三级测试卷系列答案
红果子三级测试卷系列答案 课堂练加测系列答案
课堂练加测系列答案科目:高中数学 来源: 题型:
假设要考查某企业生产的袋装牛奶质量是否达标, 现从500袋牛奶中抽取60袋进行检验, 利用随机数表抽样时, 先将500袋牛奶按000,001,  , 499进行编号. 如果从随机数表第8行第4列的数开始三位数连续向右读取, 请你依次写出最先检测的5袋牛奶的编号
, 499进行编号. 如果从随机数表第8行第4列的数开始三位数连续向右读取, 请你依次写出最先检测的5袋牛奶的编号
(下面摘取了随机数表第7行至第9行)
84 42 17 53 31 57 24 55 06 88 77 04 74 47 67 21 76 33 50 25 83 92 12 06 76
63 01 63 78 59 16 95 55 67 19 98 10 50 71 75 12 86 73 58 07 44 39 52 38 79
33 21 12 34 29 78 64 56 07 82 52 42 07 44 38 15 51 00 13 42 99 66 02 79 54
查看答案和解析>>
科目:高中数学 来源: 题型:
若( 1 + 2 ai )i = 1 - b i ,其中a 、 b ∈ R,i 是虚数单位,则| a + b i | =
A.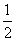 + i B.5 C.
+ i B.5 C.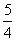 D.
D.
查看答案和解析>>
科目:高中数学 来源: 题型:
如图所示,正四棱锥P-ABCD中,O为底面正方形的中心,侧棱PA与底面ABCD所成的角的正切值为 .
.
(1)求侧面PAD与底面ABCD所成的二面角的大小;
(2)若E是PB的中点,求异面直线PD与AE所成角的正切值;
 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com