
若s i nθ+ cosθ= 2 , 则ta n( θ+ 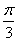 ) 的值是
) 的值是
A.1 B.- 3 - 2
C.- 1 + 3 D.- 2 - 3
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案科目:高中数学 来源: 题型:
如图,四棱锥P-ABCD中,侧面PDC是边长为2的正三角形,且与底面垂直,底面ABCD是菱形且∠ADC=60°,M为PB的中点.
(1)求PA与底面ABCD所成角的大小.
(2)求证:PA⊥平面CDM.
(3)求二面角D-MC-B的余弦值.

查看答案和解析>>
科目:高中数学 来源: 题型:
已知a > b > 0 ,椭圆 C1 的方程为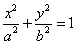 ,双曲线 C2 的方程为
,双曲线 C2 的方程为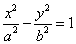 ,C1 与 C2 的离心率之积为
,C1 与 C2 的离心率之积为 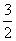 , 则 C1 、 C2 的离心率分别为
, 则 C1 、 C2 的离心率分别为
A.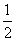 ,3 B.
,3 B.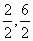 C.
C.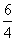 ,2 D.
,2 D.
查看答案和解析>>
科目:高中数学 来源: 题型:
在 △ABC 中,角 A, B, C 所对的边分别为a ,b ,c , 且 C =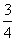 π ,s i nA =
π ,s i nA =  ,c - a = 5 - 10 , 则b = .
,c - a = 5 - 10 , 则b = .
查看答案和解析>>
科目:高中数学 来源: 题型:
已知抛物线C: x2= 2 py( p > 0) 的焦点为F , 抛物线上一点A的横坐标为x 1( x1 > 0) ,过点 A 作抛物线C 的切线l1 交x 轴于点D , 交y 轴于点Q ,交直线l ∶y =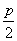 于点 M,当| FD| = 2 时,∠AF D = 60° .
于点 M,当| FD| = 2 时,∠AF D = 60° .
( Ⅰ) 求证: △AFQ 为等腰三角形, 并求抛物线 C 的方程;
( Ⅱ) 若点 B 位于y 轴左侧的抛物线C 上, 过点B 作抛物线C 的切线l2 交直线l1 于点P , 交直线l 于点 N , 求 △P MN 面积的最小值, 并求取到最小值时的x1 值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com