
【题目】如图,在四棱锥![]() 中,
中,![]() 平面
平面![]()
![]()
![]() ,
,![]() 为线段
为线段![]() 上一点不在端点.
上一点不在端点.
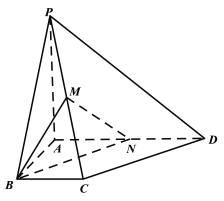
(1)当![]() 为中点时,
为中点时,![]() ,求证:
,求证:![]() 面
面![]()
(2)当![]() 为
为![]() 中点时,是否存在
中点时,是否存在![]() ,使得直线
,使得直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() ,若存在求出M的坐标,若不存在,说明理由.
,若存在求出M的坐标,若不存在,说明理由.
【答案】(1)证明见解析(2)存在,![]()
【解析】
(1)法一:建立空间直角坐标系,找坐标,利用直线的方向向量与平面的法向量垂直,证明即可.法二:取BP的中点E,连接![]() ,
,![]() ,则
,则![]() ,根据线面平行的判定定理证明即可.
,根据线面平行的判定定理证明即可.
(2)假设存在点M,根据![]() ,求点M的坐标
,求点M的坐标![]() ,求平面
,求平面![]() 的法向量为
的法向量为![]() ,根据
,根据![]() ,求解
,求解![]() ,即可.
,即可.
(1)方法一:证明:因为![]() 平面
平面![]() ,
,![]() ,
,![]() 平面
平面![]() .
.
所以![]() .
.
又![]() ,所以
,所以![]() ,
,![]() ,
,![]() 两两垂直.
两两垂直.

分别以![]() 、
、![]() 、
、![]() 所在直线为
所在直线为![]() 轴、
轴、![]() 轴、
轴、![]() 轴建立空间直角坐标系
轴建立空间直角坐标系![]() .
.
则![]() ,
,![]() .
.
显然平面![]() 的法向量为
的法向量为![]() ,则
,则![]()
又![]() 不在平面
不在平面![]() 内,所以
内,所以![]() 平面
平面![]() .
.
方法二:取![]() 的中点
的中点![]() ,连接
,连接![]() ,
,![]()

由![]() 为
为![]() 的中点,可知
的中点,可知![]()
在平面四边形![]() 中,
中,![]()
即![]() ,所以
,所以![]() ,即
,即![]()
由已知得![]()
所以![]() ,四边形
,四边形![]() 是平行四边形,所以
是平行四边形,所以![]()
因为![]() 平面
平面![]() ,
,![]() 平面
平面![]()
所以![]() 平面
平面![]()
(2)假设存在点M使得![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]()
则![]() ,所以
,所以![]()
![]()
![]() 为
为![]() 中点,则
中点,则![]() ,即
,即![]()
设平面![]() 的法向量为
的法向量为![]()
∴ ,不妨设
,不妨设![]() ,则
,则![]()
∴![]()
设线面角为![]() ,则
,则![]()
解得![]() 或1(舍去)
或1(舍去)
∴![]() 时,直线
时,直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() .
.


科目:高中数学 来源: 题型:
【题目】选修4— 4:坐标系与参数方程
设极坐标系与直角坐标系![]() 有相同的长度单位,原点
有相同的长度单位,原点![]() 为极点,
为极点,![]() 轴正半轴为极轴,曲线
轴正半轴为极轴,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 是参数),直线
是参数),直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(Ⅰ)求曲线![]() 的普通方程和直线
的普通方程和直线![]() 的参数方程;
的参数方程;
(Ⅱ)设点![]() ,若直线
,若直线![]() 与曲线
与曲线![]() 相交于
相交于![]() 两点,且
两点,且![]() ,求
,求![]() 的值﹒
的值﹒
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知三个村庄A,B,C构成一个三角形,且AB=5千米,BC=12千米,AC=13千米.为了方便市民生活,现在△ABC内任取一点M建一大型生活超市,则M到A,B,C的距离都不小于2千米的概率为
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 满足:
满足:![]() ,
,![]() (
(![]() ),数列
),数列![]() 满足:
满足:![]() ,
,![]() (
(![]() ),数列
),数列![]() 的前
的前![]() 项和为
项和为![]() .
.
(1)求数列![]() 的通项公式;
的通项公式;
(2)求证:数列![]() 是等比数列;
是等比数列;
(3)求证:数列![]() 是递增数列;若当且仅当
是递增数列;若当且仅当![]() 时,
时,![]() 取得最小值,求
取得最小值,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出四个命题:①若x2﹣3x+2=0,则x=1或x=2;②若x=y=0,则x2+y2=0;③已知x,y∈N,若x+y是奇数,则x、y中一个是奇数,一个是偶数;④若x1,x2是方程x2﹣2![]() x+2=0的两根,则x1,x2可以是一椭圆与一双曲线的离心率,那么( )
x+2=0的两根,则x1,x2可以是一椭圆与一双曲线的离心率,那么( )
A.③的否命题为假B.①的逆否命题为假
C.②的逆命题为真D.④的逆否命题为假
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在如图所示的几何体中,四边形CDEF为正方形,四边形ABCD为梯形,![]() ,
,![]() ,
,![]() ,
,![]() 平面ABCD.
平面ABCD.
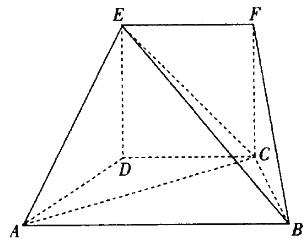
![]() 求BE与平面EAC所成角的正弦值;
求BE与平面EAC所成角的正弦值;
![]() 线段BE上是否存在点M,使平面
线段BE上是否存在点M,使平面![]() 平面DFM?若存在,求
平面DFM?若存在,求![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某机构对A市居民手机内安装的“APP”(英文Application的缩写,一般指手机软件)的个数和用途进行调研,在使用智能手机的居民中随机抽取了100人,获得了他们手机内安装APP的个数,整理得到如图所示频率分布直方图:
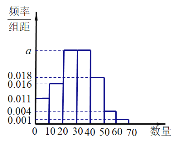
(Ⅰ)从A市随机抽取一名使用智能手机的居民,试估计该居民手机内安装APP的个数不低于30的概率;
(Ⅱ)从A市随机抽取3名使用智能手机的居民进一步做调研,用X表示这3人中手机内安装APP的个数在[20,40)的人数.
①求随机变量X的分布列及数学期望;
②用Y1表示这3人中安装APP个数低于20的人数,用Y2表示这3人中手机内安装APP的个数不低于40的人数.试比较EY1和EY2的大小.(只需写出结论)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com