
【题目】在如图所示的几何体中,四边形CDEF为正方形,四边形ABCD为梯形,![]() ,
,![]() ,
,![]() ,
,![]() 平面ABCD.
平面ABCD.
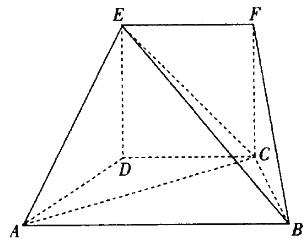
![]() 求BE与平面EAC所成角的正弦值;
求BE与平面EAC所成角的正弦值;
![]() 线段BE上是否存在点M,使平面
线段BE上是否存在点M,使平面![]() 平面DFM?若存在,求
平面DFM?若存在,求![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
【答案】(1)![]() ;(2)见解析
;(2)见解析
【解析】
![]() 以C为原点,CD为x轴,CB为y轴,CF为z轴,建立空间直角坐标系,求出平面EAC的法向量,利用向量法能求出BE与平面EAC所成角的正弦值.
以C为原点,CD为x轴,CB为y轴,CF为z轴,建立空间直角坐标系,求出平面EAC的法向量,利用向量法能求出BE与平面EAC所成角的正弦值.
![]() 设线段BE上存在点
设线段BE上存在点![]() b,
b,![]() ,
,![]() ,
,![]() ,使平面
,使平面![]() 平面DFM,求出平面DMF的法向量和平面EAC的法向量,利用向量法求出线段BE上不存在点M,使平面
平面DFM,求出平面DMF的法向量和平面EAC的法向量,利用向量法求出线段BE上不存在点M,使平面![]() 平面DFM.
平面DFM.
![]() 四边形CDEF为正方形,四边形ABCD为梯形,
四边形CDEF为正方形,四边形ABCD为梯形,![]() ,
,![]() ,
,![]() 平面ABCD.
平面ABCD.
![]() 以C为原点,CD为x轴,CB为y轴,
以C为原点,CD为x轴,CB为y轴,
CF为z轴,建立空间直角坐标系,
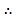
设![]() ,则
,则![]() 1,
1,![]() ,
,
![]() 0,
0,![]() ,
,![]() 1,
1,![]() ,
,
![]() 0,
0,![]() ,
,![]() 0,
0,![]() ,
,
![]() ,
,![]() 1,
1,![]() ,
,
![]() 0,
0,![]() ,
,
设平面EAC的法向量![]() y,
y,![]() ,
,
则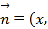 ,取
,取![]() ,
,
得![]() ,
,
设BE与平面EAC所成角为![]() ,
,
则![]() .
.
![]() 与平面EAC所成角的正弦值为
与平面EAC所成角的正弦值为![]() .
.
![]() 线段BE上不存在点M,使平面
线段BE上不存在点M,使平面![]() 平面DFM.
平面DFM.
理由如下:
设线段BE上存在点![]() b,
b,![]() ,
,![]() ,
,![]() ,使平面
,使平面![]() 平面DFM,
平面DFM,
则![]() ,
,![]() ,
,![]() ,
,![]() 0,
0,![]() ,
,
设平面DMF的法向量![]() y,
y,![]() ,
,
则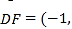 ,取
,取![]() ,得
,得![]() ,
,
![]() 平面
平面![]() 平面DFM,平面EAC的法向量
平面DFM,平面EAC的法向量![]() ,
,
![]() ,解得
,解得![]() ,
,
![]() 线段BE上不存在点M,使平面
线段BE上不存在点M,使平面![]() 平面DFM.
平面DFM.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】平面直角坐标系xOy中,已知椭圆C:![]() 1(a>b>0)的离心率为
1(a>b>0)的离心率为![]() ,左右焦点分别是F1,F2,以F1为圆心,以3为半径的圆与以F2为圆心,以1为半径的圆相交,且交点
,左右焦点分别是F1,F2,以F1为圆心,以3为半径的圆与以F2为圆心,以1为半径的圆相交,且交点![]() 在椭圆C上.
在椭圆C上.
(1)求椭圆C的方程;
(2)设椭圆E:![]() 1,P为椭圆C上任意一点,过点P的直线y=kx+m交椭圆E于A,B两点.射线PO交椭圆E于点Q.
1,P为椭圆C上任意一点,过点P的直线y=kx+m交椭圆E于A,B两点.射线PO交椭圆E于点Q.
(i)求![]() 的值,
的值,
(ii)求△ABQ面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,
中,![]() 平面
平面![]()
![]()
![]() ,
,![]() 为线段
为线段![]() 上一点不在端点.
上一点不在端点.
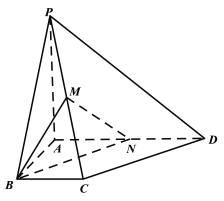
(1)当![]() 为中点时,
为中点时,![]() ,求证:
,求证:![]() 面
面![]()
(2)当![]() 为
为![]() 中点时,是否存在
中点时,是否存在![]() ,使得直线
,使得直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() ,若存在求出M的坐标,若不存在,说明理由.
,若存在求出M的坐标,若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】公安部交管局修改后的酒后违法驾驶机动车的行为分成两个档次:“酒后驾车”和“醉酒驾车”,其判断标准是驾驶人员每100毫升血液中的酒精含量X毫克,当20≤X<80时,认定为酒后驾车;当X≥80时,认定为醉酒驾车,重庆市公安局交通管理部门在对G42高速路我市路段的一次随机拦查行动中,依法检测了200辆机动车驾驶员的每100毫升血液中的酒精含量,酒精含量X(单位:毫克)的统计结果如下表:
X | [0,20) | [20,40) | [40,60) | [60,80) | [80,100) | [100,+∞) |
人数 | t | 1 | 1 | 1 | 1 | 1 |
依据上述材料回答下列问题:
(1)求t的值;
(2)从酒后违法驾车的司机中随机抽取2人,求这2人中含有醉酒驾车司机的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个经销鲜花产品的微店,为保障售出的百合花品质,每天从云南鲜花基地空运固定数量的百合花,如有剩余则免费分赠给第二天购花顾客,如果不足,则从本地鲜花供应商处进货.今年四月前10天,微店百合花的售价为每支2元,云南空运来的百合花每支进价1.6元,本地供应商处百合花每支进价1.8元,微店这10天的订单中百合花的需求量(单位:支)依次为:251,255,231,243,263,241,265,255,244,252.
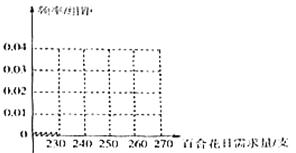
(Ⅰ)求今年四月前10天订单中百合花需求量的平均数和众数,并完成频率分布直方图;
(Ⅱ)预计四月的后20天,订单中百合花需求量的频率分布与四月前10天相同,百合花进货价格与售价均不变,请根据(Ⅰ)中频率分布直方图判断(同一组中的需求量数据用该组区间的中点值作代表,位于各区间的频率代替位于该区间的概率),微店每天从云南固定空运250支,还是255支百合花,四月后20天百合花销售总利润会更大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】a,b为空间两条互相垂直的直线,等腰直角三角形![]() 的直角边
的直角边![]() 所在直线与a,b都垂直,斜边
所在直线与a,b都垂直,斜边![]() 以
以![]() 为旋转轴选择,有下列结论:
为旋转轴选择,有下列结论:
①当直线![]() 与a成60°角时,
与a成60°角时,![]() 与b成30°角;
与b成30°角;
②当直线![]() 与a成60°角时,
与a成60°角时,![]() 与b成60°角;
与b成60°角;
③直线![]() 与a所成角的最小值为45°;
与a所成角的最小值为45°;
④直线![]() 与a所成角的最大值为60°;
与a所成角的最大值为60°;
其中正确的是_______.(填写所以正确结论的编号).
A.①③B.①④C.②③D.②④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,且经过点
,且经过点![]()
(1)求椭圆![]() 的方程;
的方程;
(2)是否存在经过点![]() 的直线
的直线![]() ,它与椭圆
,它与椭圆![]() 相交于
相交于![]() 两个不同点,且满足
两个不同点,且满足![]() 为坐标原点)关系的点
为坐标原点)关系的点![]() 也在椭圆
也在椭圆![]() 上,如果存在,求出直线
上,如果存在,求出直线![]() 的方程;如果不存在,请说明理由.
的方程;如果不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知椭圆C:![]() 1(a>b>0)的右焦点为F,A(2,0)是椭圆的右顶点,过F且垂直于x轴的直线交椭圆于P,Q两点,且|PQ|=3.
1(a>b>0)的右焦点为F,A(2,0)是椭圆的右顶点,过F且垂直于x轴的直线交椭圆于P,Q两点,且|PQ|=3.
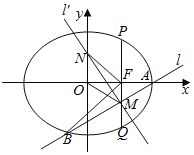
(1)求椭圆的方程;
(2)过点A的直线l与椭圆交于另一点B,垂直于l的直线l′与直线l交于点M,与y轴交于点N,若FB⊥FN且|MO|=|MA|,求直线l的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com