
【题目】在多面体![]() 中,四边形
中,四边形![]() 与
与![]() 均为正方形,
均为正方形, ![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,且
,且![]() .
.
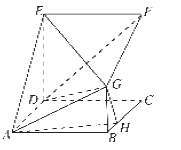
(1)求证: ![]() 平面
平面![]() ;
;
(2)求二面角![]() 的余弦值.
的余弦值.
【答案】(1)见解析(2)![]()
【解析】试题分析:(1)先根据线面垂直判定定理由线线垂直得线面垂直: ![]() 平面
平面![]() ,即得
,即得![]() 平面
平面![]() ,
, ![]() .再根据勾股定理计算可得
.再根据勾股定理计算可得![]() ,最后根据线面垂直判定定理得
,最后根据线面垂直判定定理得![]() 平面
平面![]() ;(2)利用空间向量求二面角大小:先根据条件建立恰当直角坐标系,设立各点坐标,根据方程组解出平面法向量,利用向量数量积求出两法向量夹角,最后根据法向量夹角与二面角关系得结论
;(2)利用空间向量求二面角大小:先根据条件建立恰当直角坐标系,设立各点坐标,根据方程组解出平面法向量,利用向量数量积求出两法向量夹角,最后根据法向量夹角与二面角关系得结论
试题解析:解:(1)证明:由题意可得![]() ,
, ![]() ,
,
∴![]() 平面
平面![]() ,
,
∵![]() ,
,
∴![]() 平面
平面![]() ,
,
而![]() 平面
平面![]() ,
,
∴![]() .
.
如图,连接![]() ,
,
∵![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,
,
∴![]() ,∴四边形
,∴四边形![]() 为直角梯形,
为直角梯形,
设![]() ,则依题意
,则依题意![]() ,
, ![]() ,
,
∴![]() ,
,
![]() ,
,
![]() ,
,
∴![]() .
.
∴![]() ,又
,又![]() ,
, ![]() ,
,
∴![]() 平面
平面![]() ;
;
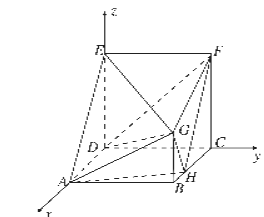
(2)解:由(1)知![]() 两两垂直,
两两垂直,
以![]() 分别为
分别为![]() 轴建立空间直角坐标系,设
轴建立空间直角坐标系,设![]() ,
,
则![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
∴![]() ,
, ![]() ,
,
设![]() 是平面
是平面![]() 的一个法向量,
的一个法向量,
则![]() ,∴
,∴![]() ,取
,取![]() ,得
,得![]() .
.
又![]() 是平面
是平面![]() 的一个法向量,
的一个法向量,
∴ ,
,
∴二面角![]() 的余弦值为
的余弦值为![]() .
.


 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案科目:高中数学 来源: 题型:
【题目】![]() 分别是定义在R上的奇函数和偶函数,当 x<0 时, f'(x)g(x)<f(x)g'(x),且 f(-3)=0 则不等式
分别是定义在R上的奇函数和偶函数,当 x<0 时, f'(x)g(x)<f(x)g'(x),且 f(-3)=0 则不等式![]() 的解集为( )
的解集为( )
A.(-∞,-3)∪(3,+∞)
B.(-3,0)∪(0,3)
C.(-3,0)∪(3,+∞)
D.(-∞,-3)∪(0,3)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某班20名同学某次数学测试的成绩可绘制成如图茎叶图.由于其中部分数据缺失,故打算根据茎叶图中的数据估计全班同学的平均成绩.


(1)完成频率分布直方图;
(2)根据(1)中的频率分布直方图估计全班同学的平均成绩![]() (同一组中的数据用改组区间的中点值作代表);
(同一组中的数据用改组区间的中点值作代表);
(3)根据茎叶图计算出的全班的平均成绩为![]() ,并假设
,并假设![]() ,且
,且![]() 取得每一个可能值的机会相等,在(2)的条件下,求概率
取得每一个可能值的机会相等,在(2)的条件下,求概率![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在正方体ABCD﹣A1B1C1D1中,点O为线段BD的中点,设点P在线段CC1上,直线OP与平面A1BD所成的角为α,则sinα的取值范围是( ) 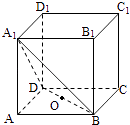
A.[ ![]() ,1]
,1]
B.[ ![]() ,1]
,1]
C.[ ![]() ,
, ![]() ]
]
D.[ ![]() ,1]
,1]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法中正确的是( ).
A.已知F1(-4,0),F2(4,0),到F1,F2两点的距离之和等于8的点的轨迹是椭圆
B.已知F1(-4,0),F2(4,0),到F1,F2两点的距离之和为6的点的轨迹是椭圆
C.到F1(-4,0),F2(4,0)两点的距离之和等于点M(5,3)到F1,F2的距离之和的点的轨迹是椭圆
D.到F1(-4,0),F2(4,0)两点距离相等的点的轨迹是椭圆
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】点E,F,G,H分别为空间四边形ABCD中AB,BC,CD,AD的中点,若AC=BD,且AC与BD成90°,则四边形EFGH是( ) 
A.菱形
B.梯形
C.正方形
D.空间四边形
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com