
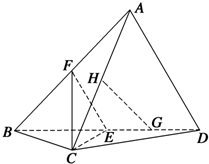
 如图,在四面体A-BCD中,F、E、H分别是棱AB、BD、AC的中点,G为DE的中点.
如图,在四面体A-BCD中,F、E、H分别是棱AB、BD、AC的中点,G为DE的中点.分析 本题考查空间立体几何线面平行的判定定理.第1题利用EF为△ABD的中位线来证明EF∥平面ACD;第2题可利用三角形相似性来证明线面平行,同时也可平面证明GHN∥平面CEF,来得到直线HG∥平面CEF.
解答 (Ⅰ)证明,如右图: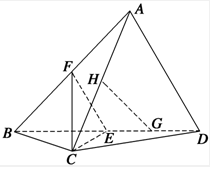
∵E、F分别为BD、BA的中点,EF为△ABD的中位线,
∴EF∥AD 且 EF=$\frac{1}{2}$AD,
∵EF?平面ACD,AD?平面ACD,
∴EF∥平面ACD;
(Ⅱ)证法一:如图,连接BH,BH与CF交于K,连接EK.
∵F、H分别是AB、AC的中点,
∴K是△ABC的重心,
∴$\frac{BK}{BH}$=$\frac{2}{3}$.
又据题设条件知,$\frac{BE}{BG}$=$\frac{2}{3}$,
∴$\frac{BK}{BH}$=$\frac{BE}{BG}$,∴EK∥GH.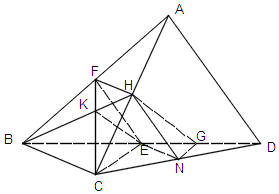
∵EK?平面CEF,GH?平面CEF,
∴直线HG∥平面CEF.
证法二如:图,取CD的中点N,连接GN、HN.
∵G为DE的中点,∴GN∥CE.
∵CE?平面CEF,GN?平面CEF,∴GN∥平面CEF.
连接FH,EN
∵F、E、H分别是棱AB、BD、AC的中点,
∴FH∥BC,EN∥BC,FH=$\frac{1}{2}BC$,EN=$\frac{1}{2}BC$∴FH∥EN,FH=EN
∴四边形FHNE为平行四边形,∴HN∥EF.
∵EF?平面CEF,HN?平面CEF,
∴HN∥平面CEF.HN∩GN=N,
∴平面GHN∥平面CEF.
∵GH?平面GHN,∴直线HG∥平面CEF.
点评 空间立体几何线面平行的判定属于高考常见题型.


 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{a}<\frac{1}{b}<0$ | B. | b2>a2 | C. | |b|>|a| | D. | b3>a3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{{\frac{a_1^2+a_2^2+…+a_n^2}{n}}}$ | B. | $\frac{{a}_{1}+{a}_{2}+…+{a}_{n}}{n}$ | ||
| C. | $\root{n}{{a}_{1}{a}_{2}…{a}_{n}}$ | D. | $\frac{n}{\frac{1}{{a}_{1}}+\frac{1}{{a}_{2}}+…+\frac{1}{{a}_{n}}}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $f(x)=3sin({\frac{x}{2}-\frac{π}{2}})$ | B. | $f(x)=3sin({\frac{x}{2}+\frac{π}{4}})$ | C. | f(x)=-3sinx | D. | f(x)=3cos2x |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com