
ЁОЬтФПЁП2019Фъ10дТ1ШеЮвЙњТЁжиМЭФюСЫНЈЙњ70жмФъЃЌЦкМфНјааСЫвЛЯЕСаДѓаЭЧьзЃЛюЖЏЃЌМЋДѓЕиМЄЗЂСЫШЋЙњШЫУёЕФАЎЙњШШЧщ.ФГаЃИпШ§бЇЩњвВЭЖШыЕНСЫетГЁАЎЙњЛюЖЏжаЃЌЫћ(Ы§)УЧРћгУжмШеанЯЂЪБМфЕНЩчЧјзівхЮёаћНВдБЃЌбЇаЃЮЊСЫЕїВщИпШ§ФаЩњКЭХЎЩњжмШеЕФЛюЖЏЪБМфЧщПіЃЌЫцЛњГщШЁСЫИпШ§ФаЩњКЭХЎЩњИї40ШЫЃЌЖдЫћ(Ы§)УЧЕФжмШеЛюЖЏЪБМфНјааСЫЭГМЦЃЌЗжБ№ЕУЕНСЫИпШ§ФаЩњЕФЛюЖЏЪБМф(ЕЅЮЛЃКаЁЪБ)ЕФЦЕЪ§ЗжВМБэКЭХЎЩњЕФЛюЖЏЪБМф(ЕЅЮЛЃКаЁЪБ)ЕФЦЕТЪЗжВМжБЗНЭМ.ЃЈЛюЖЏЪБМфОљдк![]() ФкЃЉ
ФкЃЉ
ЛюЖЏЪБМф |
|
|
|
|
|
|
ЦЕЪ§ | 8 | 10 | 7 | 9 | 4 | 2 |

ЃЈ1ЃЉИљОнЕїВщЃЌЪдХаЖЯИУаЃИпШ§ФъМЖбЇЩњжмШеЛюЖЏЪБМфНЯГЄЕФЪЧФаЩњЛЙЪЧХЎЩњЃПВЂЫЕУїРэгЩЃЛ
ЃЈ2ЃЉдкБЛГщШЁЕФ80УћИпШ§бЇЩњжаЃЌДгжмШеЛюЖЏЪБМфдк![]() ФкЕФбЇЩњжаГщШЁ2ШЫЃЌЧѓЧЁЧЩГщЕН1Фа1ХЎЕФИХТЪ.
ФкЕФбЇЩњжаГщШЁ2ШЫЃЌЧѓЧЁЧЩГщЕН1Фа1ХЎЕФИХТЪ.
ЁОД№АИЁПЃЈ1ЃЉХЎЩњЃЌРэгЩМћНтЮіЃЛЃЈ2ЃЉ![]()
ЁОНтЮіЁП
ЃЈ1ЃЉСаГіХЎЩњжмШеЛюЖЏЪБМфЦЕЪ§БэЃЌЖдБШФаЩњКЭХЎЩњЛюЖЏЪБМфЦЕЪ§БэМДПЩЕУГіНсТлЃЛ
ЃЈ2ЃЉдЫгУЙХЕфИХаЭЕФИХТЪМЦЫуЙЋЪНЧѓНтМДПЩЃЎ
НтЃКЃЈ1ЃЉИУаЃИпШ§ФъМЖжмШеЛюЖЏЪБМфНЯГЄЕФЪЧХЎЩњЃЌ
РэгЩШчЯТЃКСаГіХЎЩњжмШеЛюЖЏЪБМфЦЕЪ§Бэ
ЛюЖЏЪБМф |
|
|
|
|
|
ЦЕЪ§ | 6 | 7 | 12 | 10 | 4 |
ЖдБШФаЩњКЭХЎЩњЛюЖЏЪБМфЦЕЪ§БэЃЌПЩвдЗЂЯжЃК
ЛюЖЏЪБМфдк2аЁЪБМАЦфвдЩЯЕФФаЩњга22ШЫЃЌХЎЩњга34ШЫЃЛ
ЛюЖЏЪБМфдк3аЁЪБМАЦфвдЩЯЕФФаЩњга15ЃЌХЎЩњга26ШЫЃЛ
ЖМЪЧХЎЩњШЫЪ§ЖргкФаЩњШЫЪ§ЃЌЫљвдИУаЃИпШ§ФъМЖжмШеЛюЖЏЪБМфНЯГЄЕФЪЧХЎЩњЃЛ
ЃЈ2ЃЉБЛГщЕНЕФ80бЇЩњжажмШеЛюЖЏЪБМфдк![]() ФкЕФФаЩњга2ШЫЃЌЗжБ№МЧЮЊ
ФкЕФФаЩњга2ШЫЃЌЗжБ№МЧЮЊ![]() ЃЌ
ЃЌ![]() ЃЌХЎЩњга4ЃЌЗжБ№МЧЮЊ
ЃЌХЎЩњга4ЃЌЗжБ№МЧЮЊ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
Дгет6ШЫжаГщШЁ2.ЙВгавдЯТ15ИіЛљБОЪТМўЃЌЗжБ№ЮЊЃК
![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЛ
ЃЛ
ЦфжаЧЁЮЊ1Фа1ХЎЕФЙВга8жжЧщаЮЃЌ
ЫљвдЫљЧѓИХТЪ![]() ЃЎ
ЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГЪаЖдИпЖўбЇЩњЕФЦкФЉРэПЦЪ§бЇВтЪдЕФЪ§ОнЭГМЦЯдЪО,ШЋЪа10000УћбЇЩњЕФГЩМЈЗўДге§ЬЌЗжВМ![]() ,ЯжДгМзаЃ100ЗжвдЩЯ(КЌ100Зж)ЕФ200ЗнЪдОэжагУЯЕЭГГщбљжаЕШОрГщбљЕФЗНЗЈГщШЁСЫ20ЗнЪдОэРДЗжЮі(ЪдОэБрКХЮЊ001,002,Ё,200)ЭГМЦШчЯТ:
,ЯжДгМзаЃ100ЗжвдЩЯ(КЌ100Зж)ЕФ200ЗнЪдОэжагУЯЕЭГГщбљжаЕШОрГщбљЕФЗНЗЈГщШЁСЫ20ЗнЪдОэРДЗжЮі(ЪдОэБрКХЮЊ001,002,Ё,200)ЭГМЦШчЯТ:
ЪдОэБрКХ |
|
|
|
|
|
|
|
|
|
|
ЪдОэЕУЗж | 109 | 118 | 112 | 114 | 126 | 128 | 127 | 124 | 126 | 120 |
ЪдОэБрКХ |
|
|
|
|
|
|
|
|
|
|
ЪдОэЕУЗж | 135 | 138 | 135 | 137 | 135 | 139 | 142 | 144 | 148 | 150 |
зЂ:БэжаЪдОэБр![]()
(1)аДГіБэжаЪдОэЕУЗжЮЊ144ЗжЕФЪдОэБрКХ(аДГіОпЬхЪ§ОнМДПЩ);
(2)ИУЪагжДгвваЃжавВгУгыМзаЃЭЌбљЕФГщбљЗНЗЈГщШЁСЫ20ЗнЪдОэ,НЋМзввСНаЃет40ЗнЪдОэЕФЕУЗжжЦзїСЫОЅвЖЭМ(ШчЭМ)дкМзввСНаЃет40ЗнбЇЩњЕФЪдОэжа,ДгГЩМЈдк140ЗжвдЩЯ(КЌ140Зж)ЕФбЇЩњжаШЮвтГщШЁ3ШЫ,ИУ3ШЫдкШЋЪаХХУћЧА15УћЕФШЫЪ§МЧЮЊ![]()
![]() ЕФЗжВМСаКЭЦкЭћ.
ЕФЗжВМСаКЭЦкЭћ.
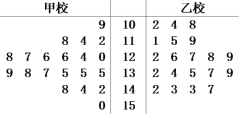
ИН:ШєЫцЛњБфСП![]() ЗўДге§ЬЌЗжВМ
ЗўДге§ЬЌЗжВМ![]() ,дђ
,дђ![]() ,
,![]() ,
,![]() .
.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
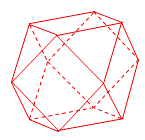
ЁОЬтФПЁПАые§ЖрУцЬх(semiregular solid)врГЦЁААЂЛљУзЕТЖрУцЬхЁБЃЌШчЭМЫљЪОЃЌЪЧгЩБпЪ§ВЛШЋЯрЭЌЕФе§ЖрБпаЮЮЊУцЕФЖрУцЬхЃЌЬхЯжСЫЪ§бЇЕФЖдГЦУРЃЎНЋе§ЗНЬхбиНЛгквЛЖЅЕуЕФШ§ЬѕРтЕФжаЕуНиШЅвЛИіШ§РтзЖЃЌШчДЫЙВПЩНиШЅАЫИіШ§РтзЖЃЌЕУЕНвЛИігаЪЎЫФИіУцЕФАые§ЖрУцЬхЃЌЫќУЧЕФБпГЄЖМЯрЕШЃЌЦфжаАЫИіЮЊе§Ш§НЧаЮЃЌСљИіЮЊе§ЗНаЮЃЌГЦетбљЕФАые§ЖрУцЬхЮЊЖўЪЎЫФЕШБпЬх.ШєЖўЪЎЫФЕШБпЬхЕФРтГЄЮЊ![]() ЃЌдђИУЖўЪЎЫФЕШБпЬхЭтНгЧђЕФБэУцЛ§ЮЊЃЈ ЃЉ
ЃЌдђИУЖўЪЎЫФЕШБпЬхЭтНгЧђЕФБэУцЛ§ЮЊЃЈ ЃЉ
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЪЎШ§НьШЋЙњШЫДѓЖўДЮЛсвщгк2019Фъ3дТ5ШедкОЉейПЊЮЊСЫСЫНтФГаЃДѓбЇЩњЖдСНЛсЕФЙизЂГЬЖШЃЌбЇаЃУНЬхдкПЊФЛКѓЕФЕкЖўЬьЃЌДгШЋаЃбЇЩњжаЫцЛњГщШЁСЫ180ШЫЃЌЖдЪЧЗёЪеПД2019ФъСНЛсПЊФЛЛсЧщПіНјааСЫЮЪОэЕїВщЃЌЭГМЦЪ§ОнШчЯТЃК
ЪеПД | УЛЪеПД | |
ФаЩњ | 80 | 40 |
ХЎЩњ | 30 | 30 |
ЃЈ1ЃЉИљОнЩЯБэЫЕУїЃЌдкЗИДэЮѓЕФИХТЪВЛГЌЙ§1%ЕФЧАЬсЯТЃЌФмЗёШЯЮЊИУаЃДѓбЇЩњЪеПДПЊФЛЛсгыадБ№гаЙиЃПЃЈМЦЫуНсЙћОЋШЗЕН0.001ЃЉ
ЃЈ2ЃЉЯжДгЫцЛњГщШЁЕФбЇЩњжаЃЌВЩгУАДадБ№ЗжВуГщбљЕФЗНЗЈбЁШЁ6ШЫЃЌРДВЮМг2019ФъСНЛсЕФжОдИепаћДЋЛюЖЏЃЌШєДгет6ШЫжаЫцЛњбЁШЁ2ШЫЕНИїАрМЖаћДЋНщЩмЃЌЧѓЧЁКУбЁЕНвЛУћФаЩњКЭвЛУћХЎЩњЕФИХТЪ. ИН ЃЌЦфжа
ЃЌЦфжа![]() .
.
| 0.10 | 0.05 | 0.025 | 0.01 | 0.005 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПгУЯИИжЙмКИНгЖјГЩЕФЛЈЬГЮЇРИЙЙМўШчЭМЫљЪОЃЌЫќЕФЭтПђЪЧвЛИіЕШбќЬнаЮPQRSЃЌФкВПЪЧвЛЖЮХзЮяЯпКЭвЛИљКсСКЃЌХзЮяЯпЕФЖЅЕугыЬнаЮЩЯЕзжаЕуЪЧКИНгЕуOЃЌЬнаЮЕФбќНєППдкХзЮяЯпЩЯЃЌСНЬѕбќЕФжаЕуЪЧЬнаЮЕФбќЁЂХзЮяЯпвдМАКсСКЕФКИНгЕуAЃЌBЃЌХзЮяЯпгыЬнаЮЯТЕзЕФСНИіКИНгЕуЮЊCЃЌDЃЌвбжЊЬнаЮЕФИпЪЧ40РхУзЃЌCЃЌDСНЕуМфЕФОрРыЮЊ40РхУзЃЎ
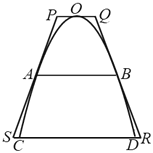
ЃЈ1ЃЉЧѓКсСКABЕФГЄЖШЃЛ
ЃЈ2ЃЉЧѓЬнаЮЭтПђЕФгУСЯГЄЖШЃЛ
ЃЈзЂЃКЯИИжЙмЕФДжЯИЕШвђЫиКіТдВЛМЦЃЌНсЙћОЋШЗЕН1РхУзЃЉ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЮЊСЫНтШЋЪаЭГПМЧщПіЃЌДгЫљгаВЮМгПМЪдЕФПМЩњжаГщШЁ4000УћПМЩњЕФГЩМЈЃЌЦЕТЪЗжВМжБЗНЭМШчЯТЭМЫљЪО.

ЃЈ1ЃЉЧѓет4000УћПМЩњЕФАыОљГЩМЈ![]() ЃЈЭЌвЛзщжаЪ§ОнгУИУзщЧјМфжаЕузїДњБэЃЉЃЛ
ЃЈЭЌвЛзщжаЪ§ОнгУИУзщЧјМфжаЕузїДњБэЃЉЃЛ
ЃЈ2ЃЉгЩжБЗНЭМПЩШЯЮЊПМЩњПМЪдГЩМЈzЗўДге§ЬЌЗжВМ![]() ЃЌЦфжа
ЃЌЦфжа![]() ЗжБ№ШЁПМЩњЕФЦНОљГЩМЈ
ЗжБ№ШЁПМЩњЕФЦНОљГЩМЈ![]() КЭПМЩњГЩМЈЕФЗНВю
КЭПМЩњГЩМЈЕФЗНВю![]() ЃЌФЧУДГщШЁЕФ4000УћПМЩњГЩМЈГЌЙ§84.81ЗжЃЈКЌ84.81ЗжЃЉЕФШЫЪ§ЙРМЦгаЖрЩйШЫЃП
ЃЌФЧУДГщШЁЕФ4000УћПМЩњГЩМЈГЌЙ§84.81ЗжЃЈКЌ84.81ЗжЃЉЕФШЫЪ§ЙРМЦгаЖрЩйШЫЃП
ЃЈ3ЃЉШчЙћгУГщШЁЕФПМЩњГЩМЈЕФЧщПіРДЙРМЦШЋЪаПМЩњЕФГЩМЈЧщПіЃЌЯжДгШЋЪаПМЩњжаЫцЛњГщШЁ4УћПМЩњЃЌМЧГЩМЈВЛГЌЙ§84.81ЗжЕФПМЩњШЫЪ§ЮЊ![]() ЃЌЧѓ
ЃЌЧѓ![]() .ЃЈОЋШЗЕН0.001ЃЉ
.ЃЈОЋШЗЕН0.001ЃЉ
ИНЃКЂй![]() ЃЛ
ЃЛ
Ђк![]() ЃЌдђ
ЃЌдђ![]() ЃЛ
ЃЛ
Ђл![]() .
.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЪ§Са![]() ЕФЪзЯю
ЕФЪзЯю![]() ЃЌЖдШЮвтЕФ
ЃЌЖдШЮвтЕФ![]() ЃЌЖМга
ЃЌЖМга![]() ЃЌЪ§Са
ЃЌЪ§Са![]() ЪЧЙЋБШВЛЮЊ
ЪЧЙЋБШВЛЮЊ![]() ЕФЕШБШЪ§Са.
ЕФЕШБШЪ§Са.
ЃЈ1ЃЉЧѓЪЕЪ§![]() ЕФжЕЃЛ
ЕФжЕЃЛ
ЃЈ2ЃЉЩш Ъ§Са
Ъ§Са![]() ЕФЧА
ЕФЧА![]() ЯюКЭЮЊ
ЯюКЭЮЊ![]() ЃЌЧѓЫљгае§ећЪ§
ЃЌЧѓЫљгае§ећЪ§![]() ЕФжЕЃЌЪЙЕУ
ЕФжЕЃЌЪЙЕУ![]() ЧЁКУЮЊЪ§Са
ЧЁКУЮЊЪ§Са![]() жаЕФЯю.
жаЕФЯю.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШєКЏЪ§fЃЈxЃЉ=Љ![]() xЉ
xЉ![]() cos2x+mЃЈsinxЉcosxЃЉдкЃЈЉЁоЃЌ+ЁоЃЉЩЯЕЅЕїЕнМѕЃЌдђmЕФШЁжЕЗЖЮЇЪЧ____________ЃЎ
cos2x+mЃЈsinxЉcosxЃЉдкЃЈЉЁоЃЌ+ЁоЃЉЩЯЕЅЕїЕнМѕЃЌдђmЕФШЁжЕЗЖЮЇЪЧ____________ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊКЏЪ§![]() .
.
ЃЈ1ЃЉЕБ![]() ЪБЃЌЧѓКЏЪ§
ЪБЃЌЧѓКЏЪ§![]() ЕФМЋжЕЃЛ
ЕФМЋжЕЃЛ
ЃЈ2ЃЉЕБ![]() ЪБЃЌЬжТлКЏЪ§
ЪБЃЌЬжТлКЏЪ§![]() ЕФЕЅЕїадЃЎ
ЕФЕЅЕїадЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com