
分析 利用同角三角函数基本关系式、诱导公式及辅助角公式化简求值.
解答 解:sin2230°+sin110°•cos80°=cos240°+cos20°sin10°
=$\frac{1}{2}+\frac{1}{2}cos80°$+cos20°sin(30°-20°)=$\frac{1}{2}+\frac{1}{2}cos80°$+cos20$°(\frac{1}{2}cos20°-\frac{\sqrt{3}}{2}sin20°)$
=$\frac{1}{2}+\frac{1}{2}cos80°+\frac{1}{2}co{s}^{2}20°-\frac{\sqrt{3}}{2}sin20°cos20°$=$\frac{1}{2}+\frac{1}{2}cos80°$$+\frac{1}{4}+\frac{1}{4}cos40°-\frac{\sqrt{3}}{4}sin40°$
=$\frac{1}{2}+\frac{1}{4}+\frac{1}{2}cos80°-\frac{1}{2}cos80°=\frac{3}{4}$.
故答案为:$\frac{3}{4}$.
点评 本题考查三角函数的化简求值,考查了同角三角函数基本关系式、诱导公式及辅助角公式的应用,体现了数学转化思想方法,是中档题.


科目:高中数学 来源: 题型:解答题
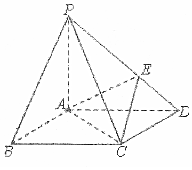 在底面是菱形的四棱锥P-ABCD中,∠ABC=60°,PA=AC=a,PB=PD=$\sqrt{2}$a,点E在PD上,且PE:ED=2:1,面PAB∩面PCD=1.
在底面是菱形的四棱锥P-ABCD中,∠ABC=60°,PA=AC=a,PB=PD=$\sqrt{2}$a,点E在PD上,且PE:ED=2:1,面PAB∩面PCD=1.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,+∞) | B. | (-1,+∞) | C. | (-∞,1) | D. | (-∞,-1) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{2}{3}$ | B. | -$\frac{3}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{3}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,10] | B. | $(\frac{1}{2},1)∪(1,5]$ | C. | $(\frac{1}{2},5]$ | D. | (1,2)∪(2,10] |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
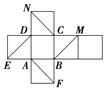 如图所示是正方体的平面展开图,在这个正方体中,其中正确的命题有( )
如图所示是正方体的平面展开图,在这个正方体中,其中正确的命题有( )| A. | ①②③ | B. | ②④ | C. | ③④ | D. | ②③④ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com