
分析 (I)利用垂直平分线的性质、椭圆的定义即可得出.
(Ⅱ)由椭圆的对称性可得,定点S必在x轴上.设直线l的方程为y=k(x-m),A(x1,y1),B(x2,y2),直线A'B与x轴的交点为S(s,0)则A'(x1,-y1),直线方程与椭圆方程联立可得:(3+4k2)x2-8k2mx+4k2m2-12=0,利用根与系数的关系,及其A',B,S三点共线,进而得出.
解答 解:(Ⅰ)由题意可知,|MP|=|MF|,∴|ME|+|MF|=4,
∵|ME|+|MF|>|EF|,
∴点M的轨迹是以点F(1,0)和E(-1,0)为焦点,2a=4的椭圆,
∴$b=\sqrt{{a^2}-{c^2}}=\sqrt{3}$,
∴曲线Γ的方程为$\frac{x^2}{4}+\frac{y^2}{3}=1$.
(Ⅱ)由椭圆的对称性可得,定点S必在x轴上.设直线l的方程为y=k(x-m),A(x1,y1),B(x2,y2),直线A'B与x轴的交点为S(s,0)则A'(x1,-y1),
∴$\overrightarrow{S{A}^{′}}$=(x1-s,-y1),$\overrightarrow{SB}$=(x2-s,y2),
由$\left\{\begin{array}{l}\frac{x^2}{4}+\frac{y^2}{3}=1\\ y=k(x-m)\end{array}\right.$得,(3+4k2)x2-8k2mx+4k2m2-12=0,
△>0,即(4-m2)k2+3>0,
∴$\left\{\begin{array}{l}{x_1}+{x_2}=\frac{{8{k^2}m}}{{3+4{k^2}}}\\{x_1}{x_2}=\frac{{4{k^2}{m^2}-12}}{{3+4{k^2}}}.\end{array}\right.$,
当k≠0时,由A',B,S三点共线,可得(x1-s)y2+(x2-s)y1=0,
即k(x1-s)(x2-m)+k(x2-s)(x1-m)=0,2x1x2-(s+m)(x1+x2)+2sm=0,
∴$AC=\sqrt{E{C^2}+A{E^2}}=2\sqrt{3}$,
∴$\frac{6sm-24}{{3+4{k^2}}}=0$,
∴$s=\frac{4}{m}$,即$S(\frac{4}{m},0)$,k=0时,直线A'B与x轴重合,过点$S(\frac{4}{m},0)$.
综上述,直线A'B恒过一个定点$S(\frac{4}{m},0)$,且$|{OS}|•|{OQ}|=\frac{4}{m}•m$=4.
点评 本题主要考查直线、椭圆、直线与椭圆的位置关系等基础知识,考查运算求解能力、推理论证能力,考查函数与方程思想、化归与转化思想,考查考生分析问题和解决问题的能力,属于难题.


 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 1 | 1 | 1 | 1 | 1 | 1 | … |
| 1 | 2 | 3 | 4 | 5 | 6 | … |
| 1 | 3 | 5 | 7 | 9 | 11 | … |
| 1 | 4 | 7 | 10 | 13 | 16 | … |
| 1 | 5 | 9 | 13 | 17 | 21 | … |
| 1 | 6 | 11 | 16 | 21 | 26 | … |
| … | … | … | … | … | … | … |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
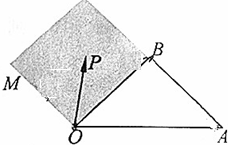 如图,OM∥AB,点P在由射线OM,线段OB及AB的延长线围成的阴影区域内(不含边界),且$\overrightarrow{OP}$=x$\overrightarrow{OA}$+y$\overrightarrow{OB}$,给出以下结论:
如图,OM∥AB,点P在由射线OM,线段OB及AB的延长线围成的阴影区域内(不含边界),且$\overrightarrow{OP}$=x$\overrightarrow{OA}$+y$\overrightarrow{OB}$,给出以下结论:查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com