
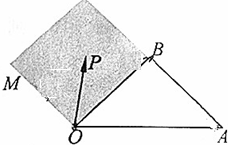
 如图,OM∥AB,点P在由射线OM,线段OB及AB的延长线围成的阴影区域内(不含边界),且$\overrightarrow{OP}$=x$\overrightarrow{OA}$+y$\overrightarrow{OB}$,给出以下结论:
如图,OM∥AB,点P在由射线OM,线段OB及AB的延长线围成的阴影区域内(不含边界),且$\overrightarrow{OP}$=x$\overrightarrow{OA}$+y$\overrightarrow{OB}$,给出以下结论:分析 结合图形,根据条件即可得到$\overrightarrow{OP}=(x+y)\overrightarrow{OB}+(-x)\overrightarrow{OM}$,从而有$\left\{\begin{array}{l}{0<x+y<1}\\{-x>0}\end{array}\right.$,这样便可判断每个结论的正误,找出正确结论的序号.
解答 解:根据条件,$\overrightarrow{OA}=\overrightarrow{OB}-\overrightarrow{OM}$;
∴$\overrightarrow{OP}=(x+y)\overrightarrow{OB}+(-x)\overrightarrow{OM}$;
点P在阴影区域,不含边界;
∴$\left\{\begin{array}{l}{0<x+y<1}\\{-x>0}\end{array}\right.$;
∴x<0,为使0<x+y<1,y的范围不会为(0,$\frac{1}{2}$);
∵P点不和B重合,∴x+y≠1;
显然,$x=-\frac{1}{2}$时,$\frac{1}{2}<y<\frac{3}{2}$;
∴①④正确.
故答案为:①④.
点评 考查向量加法的几何意义,相反向量和相等向量的概念,以及向量加法的平行四边形法则,清楚点P所在的区域.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
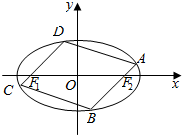 已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的短轴的一个顶点与两个焦点构成正三角形,且该三角形的面积为$\sqrt{3}$.
已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的短轴的一个顶点与两个焦点构成正三角形,且该三角形的面积为$\sqrt{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com