
分析 利用换元法设f(x)=ax+2,g(x)=x2+2b,根据一元一次函数和一元二次函数的图象和性质进行判断求解即可.
解答 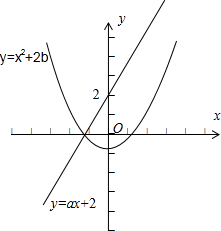 解:∵(ax+2)(x2+2b)≤0对任意x∈(-∞,0]恒成立,
解:∵(ax+2)(x2+2b)≤0对任意x∈(-∞,0]恒成立,
∴当x=0时,不等式等价为4b≤0,即b≤0,
设f(x)=ax+2恒过(0,2),g(x)=x2+2b,开口向上,
画出两个函数的图象,如图:
g(x)=x2+2b=0,可得x=-$\sqrt{-2b}$.x=$\sqrt{-2b}$(舍去).
函数f(x)=ax+2的零点为x=-$\frac{2}{a}$,
则函数f(x)在(-$\frac{2}{a}$,0)上f(x)>0,g(x)<0;
若a=0,则f(x)=2>0,而此不满足条件;
∵函数f(x)在(-∞,-$\frac{2}{a}$)上f(x)>0,g(x)<0,
可得:-$\frac{2}{a}$=-$\sqrt{-2b}$.
可得a2b=-2.
∴a2-b=a2+(-b)≥2$\sqrt{{a}^{2}(-b)}$=2$\sqrt{2}$.当且仅当a2=-b=$\sqrt{2}$时取等号.
故答案为:2$\sqrt{2}$.
点评 本题考查了函数恒成立以及分类讨论思想、转化与化归思想及运算求解能力,解题时应根据一元一次函数和一元二次函数的图象和性质,得到两个函数的零点相同,是较难的题目.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
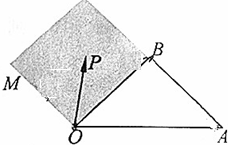 如图,OM∥AB,点P在由射线OM,线段OB及AB的延长线围成的阴影区域内(不含边界),且$\overrightarrow{OP}$=x$\overrightarrow{OA}$+y$\overrightarrow{OB}$,给出以下结论:
如图,OM∥AB,点P在由射线OM,线段OB及AB的延长线围成的阴影区域内(不含边界),且$\overrightarrow{OP}$=x$\overrightarrow{OA}$+y$\overrightarrow{OB}$,给出以下结论:查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com