
分析 (1)设一次函数f(x)=ax+b,代入已知比较系数可得a和b的方程组,解方程组可得.
(2)利用换元法设t=2x+1进行求解即可.
(3)通过配方法求出函数的解析式即可.
(4)由f(x)-2f($\frac{1}{x}$)=3x+2①,得f($\frac{1}{x}$)-2f(x)=$\frac{3}{x}$+2②,得到方程组解出f(x)即可.
解答 解:(1)设一次函数f(x)=ax+b,
则f(f(x))=a(ax+b)+b
=a2x+ab+b=4x+3,
∴$\left\{\begin{array}{l}{{a}^{2}=4}\\{ab+b=3}\end{array}\right.$,
得$\left\{\begin{array}{l}{a=2}\\{b=1}\end{array}\right.$或$\left\{\begin{array}{l}{a=-2}\\{b=-3}\end{array}\right.$,
∴f(x)=2x+1,或f(x)=-2x-3.
(2)设t=2x+1,则x=$\frac{t-1}{2}$,
则f(t)=4×($\frac{t-1}{2}$)2+8×$\frac{t-1}{2}$+3=t2+2t,
则f(x)=x2+2x.
(3)∵f(x+$\frac{1}{x}$)=x2+$\frac{1}{{x}^{2}}$-3=(x+$\frac{1}{x}$)2-5,
∴f(x)=x2-5,x∈(-∞,-2]∪[2,+∞).
(4)由f(x)-2f($\frac{1}{x}$)=3x+2①,
得f($\frac{1}{x}$)-2f(x)=$\frac{3}{x}$+2②,
由①②组成方程组,
解得:f(x)=-x-$\frac{2}{x}$-2.
点评 本题考查了求函数的解析式问题,常用方法有:配凑法,换元法,待定系数法,消元法,特殊值法等,本题属于基础题.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{PH}{HC}=\frac{1}{2}$ | B. | PH=HC | C. | $\frac{PH}{HC}=2$ | D. | 不能确定 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 1 | 1 | 1 | 1 | 1 | 1 | … |
| 1 | 2 | 3 | 4 | 5 | 6 | … |
| 1 | 3 | 5 | 7 | 9 | 11 | … |
| 1 | 4 | 7 | 10 | 13 | 16 | … |
| 1 | 5 | 9 | 13 | 17 | 21 | … |
| 1 | 6 | 11 | 16 | 21 | 26 | … |
| … | … | … | … | … | … | … |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
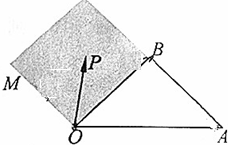 如图,OM∥AB,点P在由射线OM,线段OB及AB的延长线围成的阴影区域内(不含边界),且$\overrightarrow{OP}$=x$\overrightarrow{OA}$+y$\overrightarrow{OB}$,给出以下结论:
如图,OM∥AB,点P在由射线OM,线段OB及AB的延长线围成的阴影区域内(不含边界),且$\overrightarrow{OP}$=x$\overrightarrow{OA}$+y$\overrightarrow{OB}$,给出以下结论:查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 18 | B. | 9 | C. | 3$\sqrt{2}$ | D. | 2$\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com