
分析 (I)由题意可得:b=2,$\frac{c}{a}$=$\frac{\sqrt{5}}{5}$,a2=b2+c2,联立解得即可得出椭圆C的方程.
(II)由(I)可知:F2(1,0),且直线F2P的斜率存在,设其方程为:y=k(x-1),可得P(3,2k),设线段F2P的中点为D,则D(2,k).对k分类讨论:当k=0时,线段F2P的垂直平分线方程为:x=2.不合题意,舍去.k≠0时,线段F2P的垂直平分线为:y=-$\frac{1}{k}$(x-2)+k.与椭圆方程联立,利用相切的性质可得:△=0,解得k.可得T坐标.对k,分类讨论即可证明.
解答 解:(I)由题意可得:b=2,$\frac{c}{a}$=$\frac{\sqrt{5}}{5}$,a2=b2+c2,
联立解得b=2,a2=5,c=1.
∴椭圆C的方程为:$\frac{{x}^{2}}{5}+\frac{{y}^{2}}{4}$=1.
证明:(II)由(I)可知:F2(1,0),
且直线F2P的斜率存在,设其方程为:y=k(x-1),∴P(3,2k),
设线段F2P的中点为D,则D(2,k),
当k=0时,线段F2P的垂直平分线方程为:x=2.直线x=2与椭圆相交,不合题意,舍去.
k≠0时,线段F2P的垂直平分线为:y=-$\frac{1}{k}$(x-2)+k.联立$\left\{\begin{array}{l}{\frac{{x}^{2}}{5}+\frac{{y}^{2}}{4}=1}\\{y=-\frac{1}{k}(x-2)+k}\end{array}\right.$,化为:$(4+\frac{5}{{k}^{2}})$x2-$(\frac{20}{{k}^{2}}+10)$x+$(\frac{20}{{k}^{2}}+5{k}^{2})$=0,(*)
△=$(\frac{20}{{k}^{2}}+10)^{2}$-4$(4+\frac{5}{{k}^{2}})$$(\frac{20}{{k}^{2}}+5{k}^{2})$=$\frac{80}{{k}^{2}}$-80k2=0,解得k=±1.
(*)方程化为:9x2-30x+25=0,解得xT=$\frac{5}{3}$,代入椭圆方程可得:yT=$±\frac{4}{3}$.
当k=1时,F1(-1,0),T$(\frac{5}{3},\frac{4}{3})$,P(3,2),∵${k}_{T{F}_{1}}$=$\frac{1}{2}$,${k}_{P{F}_{1}}$=$\frac{1}{2}$,∴${k}_{T{F}_{1}}$=${k}_{P{F}_{1}}$,∴F1,T,P三点共线.
当k=-1时,F1(-1,0),T$(\frac{5}{3},-\frac{4}{3})$,P(3,-2),∵${k}_{T{F}_{1}}$=-$\frac{1}{2}$,${k}_{P{F}_{1}}$=-$\frac{1}{2}$,∴${k}_{T{F}_{1}}$=${k}_{P{F}_{1}}$,∴F1,T,P三点共线.
综上可得:F1,T,P三点共线.
点评 本题主要考查直线、椭圆、直线与椭圆的位置关系、线段垂直平分线的性质等基础知识,考查运算求解能力、推理论证能力,考查函数与方程思想、化归与转化思想,考查考生分析问题和解决问题的能力,属于难题.


 作业辅导系列答案
作业辅导系列答案 同步学典一课多练系列答案
同步学典一课多练系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 1 | 1 | 1 | 1 | 1 | 1 | … |
| 1 | 2 | 3 | 4 | 5 | 6 | … |
| 1 | 3 | 5 | 7 | 9 | 11 | … |
| 1 | 4 | 7 | 10 | 13 | 16 | … |
| 1 | 5 | 9 | 13 | 17 | 21 | … |
| 1 | 6 | 11 | 16 | 21 | 26 | … |
| … | … | … | … | … | … | … |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
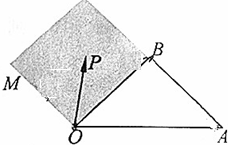 如图,OM∥AB,点P在由射线OM,线段OB及AB的延长线围成的阴影区域内(不含边界),且$\overrightarrow{OP}$=x$\overrightarrow{OA}$+y$\overrightarrow{OB}$,给出以下结论:
如图,OM∥AB,点P在由射线OM,线段OB及AB的延长线围成的阴影区域内(不含边界),且$\overrightarrow{OP}$=x$\overrightarrow{OA}$+y$\overrightarrow{OB}$,给出以下结论:查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 18 | B. | 9 | C. | 3$\sqrt{2}$ | D. | 2$\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com