
分析 (I)令f′(e2)=$\frac{1}{2}$解出m,得出f(x)的解析式,令f′(x)<0解出f(x)的单调递减区间;
(II)分离参数得出k>2x-2$\sqrt{x}$lnx(0<x<1)或k<2x-2$\sqrt{x}$lnx(x>1),分情况讨论求出右侧函数的最大值或最小值,从而得出k的范围.
解答 解:(Ⅰ) $f'(x)=\frac{m(lnx-1)}{{{{(lnx)}^2}}}$,
∵曲线y=f(x)在点(e2,f(e2))处的切线与直线2x+y=0垂直,
∴f′(e2)=$\frac{m}{4}$=$\frac{1}{2}$,
解得m=2,∴$f(x)=\frac{2x}{lnx}$,
∴$f'(x)=\frac{2(lnx-1)}{{{{(lnx)}^2}}}$,令f'(x)<0解得:0<x<1或1<x<e,
∴函数f(x)的单调减区间为(0,1)和(1,e).
(Ⅱ)∵$f(x)>\frac{k}{lnx}+2\sqrt{x}$恒成立,即$\frac{2x}{lnx}>\frac{k}{lnx}+2\sqrt{x}?\frac{k}{lnx}<\frac{2x}{lnx}-2\sqrt{x}$,
①当x∈(0,1)时,lnx<0,则$k>2x-2\sqrt{x}•lnx$恒成立,
令$g(x)=2x-2\sqrt{x}•lnx$,则g′(x)=$\frac{2\sqrt{x}-lnx-2}{\sqrt{x}}$,
再令$h(x)=2\sqrt{x}-lnx-2$,则h′(x)=$\frac{\sqrt{x}-1}{\sqrt{x}}$<0,所以h(x)在(0,1)内递减,
所以当x∈(0,1)时,h(x)>h(1)=0,故$g'(x)=\frac{h(x)}{{\sqrt{x}}}>0$,
所以g(x)在(0,1)内递增,g(x)<g(1)=2
∴k≥2.
②当x∈(1,+∞)时,lnx>0,则$k<2x-2\sqrt{x}•lnx$恒成立,
由①可知,当x∈(1,+∞)时,h'(x)>0,所以h(x)在(1,+∞)内递增,
所以当x∈(1,+∞)时,h(x)>h(1)=0,故$g'(x)=\frac{h(x)}{{\sqrt{x}}}>0$,
所以g(x)在(1,+∞)内递增,g(x)>g(1)=2⇒k≤2;
综合①②可得:k=2.
点评 本题考查了导数与函数单调性的关系,导数的几何意义,函数恒成立问题,属于中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
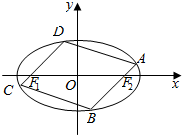 已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的短轴的一个顶点与两个焦点构成正三角形,且该三角形的面积为$\sqrt{3}$.
已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的短轴的一个顶点与两个焦点构成正三角形,且该三角形的面积为$\sqrt{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com