Question

2．在平行六面体ABCD-A${\;}_{{1}_{\;}}$B₁C₁D₁中，$\overrightarrow{A{C}_{1}}$=x$\overrightarrow{AB}$+2y$\overrightarrow{BC}$+3z$\overrightarrow{{C}_{1}C}$，则x+y+z=（　　）

• A． 1
• B． $\frac{7}{6}$
• C． $\frac{5}{6}$
• D． $\frac{2}{3}$

Answer 1

分析 如图所示，在平行六面体ABCD-A${\;}_{{1}_{\;}}$B₁C₁D₁中，$\overrightarrow{A{C}_{1}}$=$\overrightarrow{AB}$+$\overrightarrow{BC}$+$\overrightarrow{C{C}_{1}}$=$\overrightarrow{AB}$+$\overrightarrow{BC}$-$\overrightarrow{{C}_{1}C}$，与$\overrightarrow{A{C}_{1}}$=x$\overrightarrow{AB}$+2y$\overrightarrow{BC}$+3z$\overrightarrow{{C}_{1}C}$比较即可得出．

解答 解：如图所示，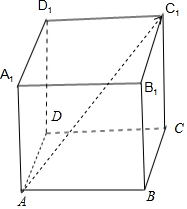
在平行六面体ABCD-A${\;}_{{1}_{\;}}$B₁C₁D₁中，
$\overrightarrow{A{C}_{1}}$=$\overrightarrow{AB}$+$\overrightarrow{BC}$+$\overrightarrow{C{C}_{1}}$=$\overrightarrow{AB}$+$\overrightarrow{BC}$-$\overrightarrow{{C}_{1}C}$，
与$\overrightarrow{A{C}_{1}}$=x$\overrightarrow{AB}$+2y$\overrightarrow{BC}$+3z$\overrightarrow{{C}_{1}C}$比较可得：
x=1，2y=1，-1=3z．
则x+y+z=1+$\frac{1}{2}$-$\frac{1}{3}$=$\frac{7}{6}$．
故选：B．

点评 本题考查了空间平行六面体法则、空间向量基本定理、数形结合方法，考查了推理能力与计算能力，属于基础题．