
【题目】随着人口老龄化的到来,我国的劳动力人口在不断减少,“延迟退休”已经成为人们越来越关注的话题,为了解公众对“延迟退休”的态度,某校课外研究性学习小组在某社区随机抽取了50人进行调查,将调查情况进行整理后制成下表:
年龄 | [20,25) | [25,30) | [30,35) | [35,40) | [40,45) |
人数 | 4 | 5 | 8 | 5 | 3 |
年龄 | [45,50) | [50,55) | [55,60) | [60,65) | [65,70) |
人数 | 6 | 7 | 3 | 5 | 4 |
经调查年龄在[25,30),[55,60)的被调查者中赞成“延迟退休”的人数分别是3人和2人.现从这两组的被调查者中各随机选取2人,进行跟踪调查.
(I)求年龄在[25,30)的被调查者中选取的2人都赞成“延迟退休”的概率;
(II)若选中的4人中,不赞成“延迟退休”的人数为![]() ,求随机变量
,求随机变量![]() 的分布列和数学期望.
的分布列和数学期望.

科目:高中数学 来源: 题型:
【题目】如图, ![]() 是半圆
是半圆![]() 的直径,
的直径, ![]() 是半圆
是半圆![]() 上除
上除![]() 、
、![]() 外的一个动点,
外的一个动点, ![]() 垂直于半圆
垂直于半圆![]() 所在的平面,
所在的平面, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
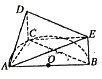
(1)证明:平面![]() 平面
平面![]() ;
;
(2)当三棱锥![]() 体积最大时,求二面角
体积最大时,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
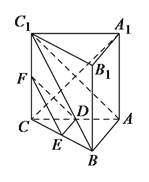
【题目】如图,在三棱柱![]() 中,
中,![]() 底面
底面![]() ,
,![]()
![]() ,
,![]() 、
、![]() 分别是棱
分别是棱![]() 、
、![]() 的中点.
的中点.
(Ⅰ)求证:![]() 平面
平面![]() .
.
(Ⅱ)若线段![]() 上的点
上的点![]() 满足平面
满足平面![]() 平面
平面![]() ,试确定点
,试确定点![]() 的位置,并说明理由.
的位置,并说明理由.
(Ⅲ)证明:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|cosx|sinx,给出下列四个说法:
①f(x)为奇函数; ②f(x)的一条对称轴为x= ![]() ;
;
③f(x)的最小正周期为π; ④f(x)在区间[﹣ ![]() ,
, ![]() ]上单调递增;
]上单调递增;
⑤f(x)的图象关于点(﹣ ![]() ,0)成中心对称.
,0)成中心对称.
其中正确说法的序号是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对某地区儿童的身高与体重的一组数据,我们用两种模型①![]() ,②
,②![]() 拟合,得到回归方程分别为
拟合,得到回归方程分别为![]() ,
, ![]() ,作残差分析,如表:
,作残差分析,如表:
身高 | 60 | 70 | 80 | 90 | 100 | 110 |
体重 | 6 | 8 | 10 | 14 | 15 | 18 |
| 0.41 | 0.01 | 1.21 | -0.19 | 0.41 | |
| -0.36 | 0.07 | 0.12 | 1.69 | -0.34 | -1.12 |
(Ⅰ)求表中空格内的值;
(Ⅱ)根据残差比较模型①,②的拟合效果,决定选择哪个模型;
(Ⅲ)残差大于![]() 的样本点被认为是异常数据,应剔除,剔除后对(Ⅱ)所选择的模型重新建立回归方程.
的样本点被认为是异常数据,应剔除,剔除后对(Ⅱ)所选择的模型重新建立回归方程.
(结果保留到小数点后两位)
附:对于一组数据![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘法估计分别为
的斜率和截距的最小二乘法估计分别为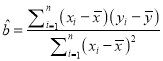 ,
, ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,棱柱ABC﹣A1B1C1的侧面BCC1B1是菱形,B1C⊥A1B 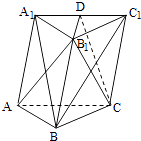
(1)证明:平面AB1C⊥平面A1BC1;
(2)设D是A1C1上的点,且A1B∥平面B1CD,求A1D:DC1的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com