
【题目】已知函数f(x)=|cosx|sinx,给出下列四个说法:
①f(x)为奇函数; ②f(x)的一条对称轴为x= ![]() ;
;
③f(x)的最小正周期为π; ④f(x)在区间[﹣ ![]() ,
, ![]() ]上单调递增;
]上单调递增;
⑤f(x)的图象关于点(﹣ ![]() ,0)成中心对称.
,0)成中心对称.
其中正确说法的序号是 .
【答案】①②④
【解析】解:函数f(x)=|cosx|sinx= 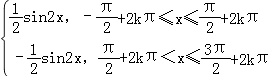 (k∈Z),
(k∈Z),
①、f(﹣x)=|cos(﹣x)|sin(﹣x)=﹣|cosx|sinx=﹣f(x),
则f(x)是奇函数,①正确;
②、∵f(π﹣x)=|cos(π﹣x)|sin(π﹣x)=|﹣cosx|sinx=f(x),
∴f(x)的一条对称轴为x= ![]() ,②正确;
,②正确;
③、∵f(π+x)=|cos(π+x)|sin(π+x)=|﹣cosx|(﹣sinx)=﹣f(x)≠f(x),
∴f(x)的最小正周期不是π,③不正确;
④、∵x∈[﹣ ![]() ,
, ![]() ],∴f(x)=|cosx|sinx=
],∴f(x)=|cosx|sinx= ![]() sin2x,且2x∈[﹣
sin2x,且2x∈[﹣ ![]() ,
, ![]() ],
],
∴f(x)在区间[﹣ ![]() ,
, ![]() ]上单调递增,④正确;
]上单调递增,④正确;
⑤、∵f(﹣π﹣x)=|cos(﹣π﹣x)|sin(﹣π﹣x)=|﹣cosx|sinx=f(x)≠﹣f(x),
∴f(x)的图象不关于点(﹣ ![]() ,0)成中心对称,⑤不正确;
,0)成中心对称,⑤不正确;
所以答案是:①②④.
【考点精析】解答此题的关键在于理解命题的真假判断与应用的相关知识,掌握两个命题互为逆否命题,它们有相同的真假性;两个命题为互逆命题或互否命题,它们的真假性没有关系.


 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案科目:高中数学 来源: 题型:
【题目】某网站针对2015年中国好声音歌手A,B,C三人进行网上投票,结果如下
观众年龄 | 支持A | 支持B | 支持C |
20岁以下 | 100 | 200 | 600 |
20岁以上(含20岁) | 100 | 100 | 400 |
(1)在所有参与该活动的人中,用分层抽样的方法抽取n人,其中有6人支持A,求n的值.
(2)在支持C的人中,用分层抽样的方法抽取5人作为一个总体,从这5人中任意选取2人,求恰有1人在20岁以下的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】平面内有向量 ![]() =(1,7),
=(1,7), ![]() =(5,1),
=(5,1), ![]() =(2,1),点X为直线OP上的一个动点.
=(2,1),点X为直线OP上的一个动点.
(1)当 ![]()
![]() 取最小值时,求
取最小值时,求 ![]() 的坐标;
的坐标;
(2)当点X满足(1)的条件和结论时,求cos∠AXB的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(文)已知矩形ABB1A1是圆柱体的轴截面,O、O1分别是下底面圆和上底面圆的圆心,母线长与底面圆的直径长之比为2:1,且该圆柱体的体积为32π,如图所示. 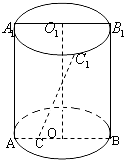
(1)求圆柱体的侧面积S侧的值;
(2)若C1是半圆弧 ![]() 的中点,点C在半径OA上,且OC=
的中点,点C在半径OA上,且OC= ![]() OA,异面直线CC1与BB1所成的角为θ,求sinθ的值.
OA,异面直线CC1与BB1所成的角为θ,求sinθ的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的前n项和为Tn= ![]() n2﹣
n2﹣ ![]() n,且an+2+3log4bn=0(n∈N*)
n,且an+2+3log4bn=0(n∈N*)
(1)求{bn}的通项公式;
(2)数列{cn}满足cn=anbn , 求数列{cn}的前n项和Sn;
(3)若cn≤ ![]() m2+m﹣1对一切正整数n恒成立,求实数m的取值范围.
m2+m﹣1对一切正整数n恒成立,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图:已知四棱锥P﹣ABCD中,PD⊥平面ABCD,ABCD是正方形,E是PA的中点,求证: 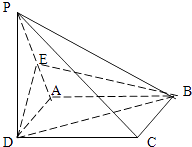
(1)PC∥平面EBD.
(2)平面PBC⊥平面PCD.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着人口老龄化的到来,我国的劳动力人口在不断减少,“延迟退休”已经成为人们越来越关注的话题,为了解公众对“延迟退休”的态度,某校课外研究性学习小组在某社区随机抽取了50人进行调查,将调查情况进行整理后制成下表:
年龄 | [20,25) | [25,30) | [30,35) | [35,40) | [40,45) |
人数 | 4 | 5 | 8 | 5 | 3 |
年龄 | [45,50) | [50,55) | [55,60) | [60,65) | [65,70) |
人数 | 6 | 7 | 3 | 5 | 4 |
经调查年龄在[25,30),[55,60)的被调查者中赞成“延迟退休”的人数分别是3人和2人.现从这两组的被调查者中各随机选取2人,进行跟踪调查.
(I)求年龄在[25,30)的被调查者中选取的2人都赞成“延迟退休”的概率;
(II)若选中的4人中,不赞成“延迟退休”的人数为![]() ,求随机变量
,求随机变量![]() 的分布列和数学期望.
的分布列和数学期望.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() 和直线
和直线![]() ,直线
,直线![]() ,
, ![]() 都经过圆
都经过圆![]() 外定点
外定点![]() .
.
(1)若直线![]() 与圆
与圆![]() 相切,求直线
相切,求直线![]() 的方程;
的方程;
(2)若直线![]() 与圆
与圆![]() 相交于
相交于![]() 两点,与
两点,与![]() 交于
交于![]() 点,且线段
点,且线段![]() 的中点为
的中点为![]() ,
,
求证: ![]() 为定值.
为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
: ![]() (
(![]() )过点
)过点![]() ,且离心率为
,且离心率为![]() ,过点
,过点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
, ![]() 两点.
两点.
(Ⅰ)求椭圆的![]() 的标准方程;
的标准方程;
(Ⅱ)已知![]() 为坐标原点,且
为坐标原点,且![]() ,求
,求![]() 面积的最大值以及此时直线
面积的最大值以及此时直线![]() 的方程.
的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com