【题目】如图，棱柱ABC﹣A1B1C1的侧面BCC1B1是菱形，B1C⊥A1B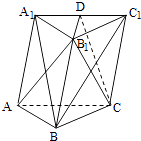 
（1）证明：平面AB1C⊥平面A1BC1；
（2）设D是A1C1上的点，且A1B∥平面B1CD，求A1D：DC1的值．
【答案】
（1）证明：因为侧面BCC1B1是菱形，所以B1C⊥BC1
又已知B1C⊥A1B，且A1B∩BC1=B，
又B1C⊥平面A1BC1，又B1C平面AB1C，
所以平面AB1C⊥平面A1BC1．
（2）解：设BC1交B1C于点E，连接DE，
则DE是平面A1BC1与平面B1CD的交线，
因为A1B∥平面B1CD，所以A1B∥DE．
又E是BC1的中点，所以D为A1C1的中点．
即A1D：DC1=1．
【解析】（1）证明平面AB1C内的直线B1C垂直平面A1BC1 ， 内的两条相交直线A1B，BC1 ， 即可证明平面AB1C⊥平面A1BC1；（2）D是A1C1上的点，且A1B∥平面B1CD，BC1交B1C于点E，连接DE，E是BC1的中点，推出D为A1C1的中点，可得A1D：DC1的值．
【考点精析】认真审题，首先需要了解直线与平面平行的性质(一条直线与一个平面平行，则过这条直线的任一平面与此平面的交线与该直线平行;简记为：线面平行则线线平行)，还要掌握平面与平面垂直的判定(一个平面过另一个平面的垂线，则这两个平面垂直)的相关知识才是答题的关键．
科目：高中数学 来源： 题型：
【题目】随着人口老龄化的到来，我国的劳动力人口在不断减少，“延迟退休”已经成为人们越来越关注的话题，为了解公众对“延迟退休”的态度，某校课外研究性学习小组在某社区随机抽取了50人进行调查，将调查情况进行整理后制成下表：
年龄 | [20,25) | [25,30) | [30,35) | [35,40) | [40,45) |
人数 | 4 | 5 | 8 | 5 | 3 |
年龄 | [45,50) | [50,55) | [55,60) | [60,65) | [65,70) |
人数 | 6 | 7 | 3 | 5 | 4 |
经调查年龄在［25,30),[55,60）的被调查者中赞成“延迟退休”的人数分别是3人和2人.现从这两组的被调查者中各随机选取2人，进行跟踪调查．
（I）求年龄在［25,30）的被调查者中选取的2人都赞成“延迟退休”的概率；
（II）若选中的4人中，不赞成“延迟退休”的人数为
，求随机变量
的分布列和数学期望．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，|φ|＜π）的一段图象如图所示．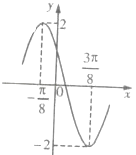 
（1）求函数f（x）的解析式；
（2）求函数f（x）的单调增区间；
（3）求函数f（x）在[﹣ 
， 
]上的单调减区间．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知椭圆
： 
（
）过点
，且离心率为
，过点
的直线
与椭圆
交于
， 
两点.
（Ⅰ）求椭圆的
的标准方程；
（Ⅱ）已知
为坐标原点，且
，求
面积的最大值以及此时直线
的方程.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】在长方体
中，
，
是棱
上的一点．
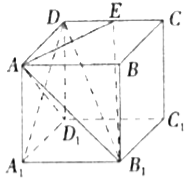
（1）求证：
平面
；
（2）求证：
；
（3）若
是棱
的中点，在棱
上是否存在点
，使得
平面
？若存在，求出线段
的长；若不存在，请说明理由．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】选修4-4：坐标系与参数方程
在平面直角坐标系中，直线
的参数方程为
，其中
为参数， 
，再以坐标原点
为极点，以
轴正半轴为极轴，建立极坐标系，曲线
的极坐标方程为
，其中
， 
，直线
与曲线
交于
两点.
（1）求
的值；
（2）已知点
，且
，求直线
的普通方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
