
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系中,直线![]() 的参数方程为
的参数方程为![]() ,其中
,其中![]() 为参数,
为参数, ![]() ,再以坐标原点
,再以坐标原点![]() 为极点,以
为极点,以![]() 轴正半轴为极轴,建立极坐标系,曲线
轴正半轴为极轴,建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() ,其中
,其中![]() ,
, ![]() ,直线
,直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点.
两点.
(1)求![]() 的值;
的值;
(2)已知点![]() ,且
,且![]() ,求直线
,求直线![]() 的普通方程.
的普通方程.
 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案科目:高中数学 来源: 题型:
【题目】如图,棱柱ABC﹣A1B1C1的侧面BCC1B1是菱形,B1C⊥A1B 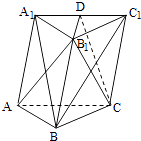
(1)证明:平面AB1C⊥平面A1BC1;
(2)设D是A1C1上的点,且A1B∥平面B1CD,求A1D:DC1的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在2016年龙岩市初中体育中考中,随意抽取某校5位同学一分钟跳绳的次数分别为:158,160,154,158,170,则由这组数据得到的结论错误的是( )
A.平均数为160
B.中位数为158
C.众数为158
D.方差为20.3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,三棱柱![]() 中,侧面
中,侧面![]() 底面
底面![]() ,
,![]() ,
,![]() ,且
,且![]() ,点
,点![]() ,
,![]() ,
,![]() 分别为
分别为![]() ,
,![]() ,
,![]() 的中点.
的中点.

(Ⅰ)求证:![]() 平面
平面![]() .
.
(Ⅱ)求证:![]() 平面
平面![]() .
.
(Ⅲ)写出四棱锥![]() 的体积.(只写出结论,不需要说明理由)
的体积.(只写出结论,不需要说明理由)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】图1是某公交公司1路车从起点站A站途经B站和C站,最终到达终点站D站的格点站路线图.(8×8的格点图是由边长为1的小正方形组成)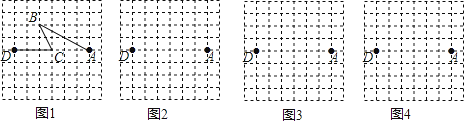
(1)求1路车从A站到D站所走的路程(精确到0.1);
(2)在图2、图3和图4的网格中各画出一种从A站到D站的路线图.(要求:①与图1路线不同、路程相同;②途中必须经过两个格点站;③所画路线图不重复)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】小丽今天晚自习准备复习历史、地理或政治中的一科,她用数学游戏的结果来决定选哪一科,游戏规则是:在平面直角坐标系中,以原点![]() 为起点,再分别以
为起点,再分别以![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 这5个点为终点,得到5个向量,任取其中两个向量,计算这两个向量的数量积
这5个点为终点,得到5个向量,任取其中两个向量,计算这两个向量的数量积![]() ,若
,若![]() ,就复习历史,若
,就复习历史,若![]() ,就复习地理,若
,就复习地理,若![]() ,就复习政治.
,就复习政治.
(1)写出![]() 的所有可能取值;
的所有可能取值;
(2)求小丽复习历史的概率和复习地理的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】【河南省豫南九校(中原名校)2017届高三下学期质量考评八数学(文)】已知双曲线![]() 的左右两个顶点是
的左右两个顶点是![]() ,
, ![]() ,曲线
,曲线![]() 上的动点
上的动点![]() 关于
关于![]() 轴对称,直线
轴对称,直线![]() 与
与![]() 交于点
交于点![]() ,
,
(1)求动点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)点![]() ,轨迹
,轨迹![]() 上的点
上的点![]() 满足
满足![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com